如图所示,质量为m=1.00㎏的带电小球用长为l=1.00m的绝缘细线悬挂于竖直向上的匀强电场中的O点,O点距水平地面的高度为h=2.05m,小球静止时细线拉力为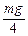 。若保持匀强电场的大小不变,而将方向缓慢转向水平向右,当小球再次静止时,求:
。若保持匀强电场的大小不变,而将方向缓慢转向水平向右,当小球再次静止时,求:
(1)细线与竖直方向的夹角?
(2)若将细线烧断,请说出小球到达地面前的运动轨迹,并求出烧断细线后小球到达地面的时间?(假设地面上方的匀强电场范围足够大)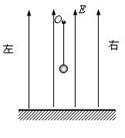
如图所示,质量为m=1.00㎏的带电小球用长为l=1.00m的绝缘细线悬挂于竖直向上的匀强电场中的O点,O点距水平地面的高度为h=2.05m,小球静止时细线拉力为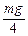 。若保持匀强电场的大小不变,而将方向缓慢转向水平向右,当小球再次静止时,求:
。若保持匀强电场的大小不变,而将方向缓慢转向水平向右,当小球再次静止时,求:
(1)细线与竖直方向的夹角?
(2)若将细线烧断,请说出小球到达地面前的运动轨迹,并求出烧断细线后小球到达地面的时间?(假设地面上方的匀强电场范围足够大)