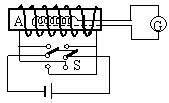
如图所示是一种测量通电螺线管中磁场的装置，把一个很小的测量线圈A放在待测处，线圈与测量电量的冲击电流计G串联，当用双刀双掷开关S使螺线管的电流反向时，测量线圈中就产生感应电动势，从而引起电荷的迁移，由表G测出电量Q，就可以算出线圈所在处的磁感应强度B。已知测量线圈共有N匝，直径为d，它和表G串联电路的总电阻为R，则被测处的磁感强度B为多大？