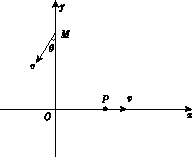
如图所示，在y轴右方有方向垂直于纸面的匀强磁场，一个质量为m，电量为q的质子以速度v水平向右经过x轴上的P点最后从y轴上的M点射出，已知M点到原点的距离为L，质子射出磁场时的速度方向与y轴的夹角θ为30°。求：
(1)磁感应强度的大小和方向；
(2)若质子在磁场中运动的适当时候，在y轴右方再加一个匀强电场，可以使质子能平行于y轴正方向做匀速直线运动。从质子经过P点开始计时，经过多长时间开始加这个匀强电场？电场强度多大？方向如何？