一个初速度为V0的匀加速直线运动,可以看成是在同一直线上的两个直线运动的合运动:一个是速度为V0的匀速直线运动,另一个是初速度为零的匀加速直线运动。合运动的速度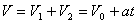 。试用将初速度V0分解成同一直线上的两个分运动V01、V02 的方法研究下面的问题。如图所示,在空间有一个与水平面平行且垂直纸面向里的足够大的匀强磁场
。试用将初速度V0分解成同一直线上的两个分运动V01、V02 的方法研究下面的问题。如图所示,在空间有一个与水平面平行且垂直纸面向里的足够大的匀强磁场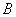 。在磁场区域有
。在磁场区域有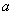 、
、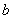 两点,相距为
两点,相距为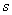 ,
,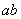 连线在水平面上且与磁场方向垂直。一质量为
连线在水平面上且与磁场方向垂直。一质量为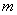 、电量为
、电量为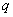 (
(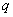
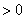 )的粒子从
)的粒子从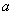 点以初速度
点以初速度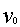 对着
对着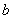 点射出,为使粒子能经过
点射出,为使粒子能经过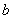 点,试问
点,试问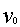 可取什么值?
可取什么值?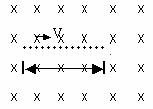
一个初速度为V0的匀加速直线运动,可以看成是在同一直线上的两个直线运动的合运动:一个是速度为V0的匀速直线运动,另一个是初速度为零的匀加速直线运动。合运动的速度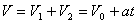 。试用将初速度V0分解成同一直线上的两个分运动V01、V02 的方法研究下面的问题。如图所示,在空间有一个与水平面平行且垂直纸面向里的足够大的匀强磁场
。试用将初速度V0分解成同一直线上的两个分运动V01、V02 的方法研究下面的问题。如图所示,在空间有一个与水平面平行且垂直纸面向里的足够大的匀强磁场 。在磁场区域有
。在磁场区域有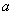 、
、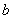 两点,相距为
两点,相距为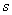 ,
,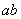 连线在水平面上且与磁场方向垂直。一质量为
连线在水平面上且与磁场方向垂直。一质量为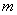 、电量为
、电量为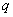 (
(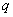
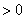 )的粒子从
)的粒子从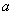 点以初速度
点以初速度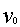 对着
对着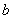 点射出,为使粒子能经过
点射出,为使粒子能经过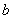 点,试问
点,试问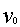 可取什么值?
可取什么值?