1935年在前苏联的一条直铁轨上,有一列火车因蒸汽不足而停驶,驾驶员将货车厢甲留在现场,只拖着几节车厢向前不远的车站开进,但他忘了将货车车厢刹好,以致货车厢在斜坡上以4 m/s的速度匀速后退,此时另一列火车乙正在以速度16 m/s向该货车厢驶来,驾驶技术相当好的驾驶员波尔西列夫立即刹车,紧接着加速倒退,结果恰好接住了货车厢甲,从而避免了相撞。设列车乙刹车过程和加速倒退过程均为匀变速直线运动,且加速度大小均为2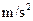 ,求波尔西列夫发现货车厢甲向自己驶来而立即开始刹车时,两车相距多远?
,求波尔西列夫发现货车厢甲向自己驶来而立即开始刹车时,两车相距多远?
1935年在前苏联的一条直铁轨上,有一列火车因蒸汽不足而停驶,驾驶员将货车厢甲留在现场,只拖着几节车厢向前不远的车站开进,但他忘了将货车车厢刹好,以致货车厢在斜坡上以4 m/s的速度匀速后退,此时另一列火车乙正在以速度16 m/s向该货车厢驶来,驾驶技术相当好的驾驶员波尔西列夫立即刹车,紧接着加速倒退,结果恰好接住了货车厢甲,从而避免了相撞。设列车乙刹车过程和加速倒退过程均为匀变速直线运动,且加速度大小均为2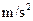 ,求波尔西列夫发现货车厢甲向自己驶来而立即开始刹车时,两车相距多远?
,求波尔西列夫发现货车厢甲向自己驶来而立即开始刹车时,两车相距多远?