重庆市万州区岩口复兴学校九年级下学期期中命题三数学试卷
据报道,重庆市九龙坡区2013年GDP总量约为770亿元,用科学记数法表示这一数据应为 ( )元。
A. 元 元 |
B. 元 元 |
C. 元 元 |
D. 元 元 |
在Rt△ABC中,∠C=90°,AC=9,BC=12,则点C到AB的距离是( )。
A. |
B. |
C. |
D. |
在数-1,1,2中任取两个数作为点坐标,那么该点刚好在一次函数 图象上的概率是( )。
图象上的概率是( )。
A. |
B. |
C. |
D. |
如图,在△ABC中,分别以点A和点B为圆心,大于 AB的长为半径画孤,两弧相交于点M,N,作直线MN,交BC于点D,连接AD.若△ADC的周长为10,AB=7,则△ABC的周长为( )。
AB的长为半径画孤,两弧相交于点M,N,作直线MN,交BC于点D,连接AD.若△ADC的周长为10,AB=7,则△ABC的周长为( )。
A、7 B、14 C、17 D、20
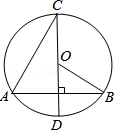
如图,在⊙O中,直径CD垂直于弦AB,若∠C=25°,则∠ABO的度数是( )。
| A.25° | B.30° | C.40° | D.50° |
2013年4月20日08时02分在四川雅安芦山县发生7.0级地震,人民生命财产遭受重大损失.某部队接到上级命令,乘车前往灾区救援,前进一段路程后,由于道路受阻,车辆无法通行,通过短暂休整后决定步行前往.则能反映部队与灾区的距离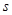 (千米)与时间
(千米)与时间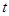 (小时)之间函数关系的大致图象是( )。
(小时)之间函数关系的大致图象是( )。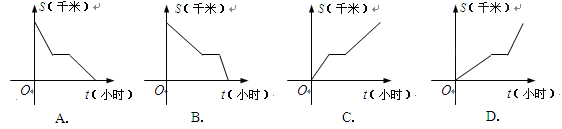
用边长相等的黑色正三角形与白色正六边形镶嵌图案,按图①②③所示的规律依次下去,则第n个图案中,所包含的黑色正三角形和白色正六边形的个数总和是( )。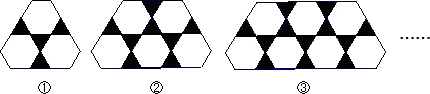
A.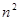 +4n+2 +4n+2 |
B.6n+1 | C.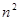 +3n+3 +3n+3 |
D.2n+4 |
如图,抛物线y=ax2+bx+c与x轴交于点A(﹣1,0),顶点坐标为(1,n),与y轴的交点在(0,2)、(0,3)之间(包含端点),则下列结论:①当x>3时,y<0;②3a+b>0;③﹣1≤a≤﹣ ;④3≤n≤4中,正确的是( )。
;④3≤n≤4中,正确的是( )。
| A.①② | B.③④ | C.①④ | D.①③ |
我校为帮扶学校的留守儿童举行了捐款活动,初三(1)班第一小组八名同学捐款数额(元)分别为:20,50,30,10,50,100,30,50.则这组数据的中位数是__________。
如果关于x的不等式组: ,的整数解仅有1,2,那么适合这个不等式组的整数a,b组成的有序数对[a,b]共有 个。
,的整数解仅有1,2,那么适合这个不等式组的整数a,b组成的有序数对[a,b]共有 个。
如图,在矩形ABCD中,AB=2DA,以点A为圆心,AB为半径的圆弧交DC于点E,交AD的延长线于点F,设DA=2,图中阴影部分的面积为 。
王老师骑自行车在环城公路上匀速行驶,每隔6分钟有一辆环湖大巴从对面向后开过,每隔30分钟又有一辆环湖大巴从后面向前开过,若环湖大巴也是匀速行驶,且不计乘客上、下车的时间,那么起点站每隔 分钟开出一辆环湖大巴。
如图,△ABC为等腰直角三角形,∠BAC=90°,BC=2,E为AB上任意一动点,以CE为斜边作等腰Rt△CDE,连接AD,下列说法:
①∠BCE=∠ACD;②AC⊥ED;③△AED∽△ECB;④AD∥BC;⑤四边形ABCD的面积有最大值,且最大值为 .其中,正确的结论是 。
.其中,正确的结论是 。
| A.①②④ | B.①③⑤ | C.②③④ | D.①④⑤ |

如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A,B的坐标分别是A(3,3)、B(1,2),△AOB绕点O逆时针旋转90°后得到△ .
.
(1)画出△ ,直接写出点
,直接写出点 ,
, 的坐标;
的坐标;
(2)在旋转过程中,点B经过的路径的长;
(3)求在旋转过程中,线段AB所扫过的面积.
“中国梦”关乎每个人的幸福生活,为进一步感知我们身边的幸福,展现万州人追梦的风采,我区某校开展了以“梦想中国,逐梦万州”为主题的摄影大赛,要求参赛学生每人交一件作品.现将参赛的50件作品的成绩(单位:分)进行统计如下:
| 等级 |
成绩(用s表示) |
频数 |
频率 |
| A |
90≤s≤100 |
x |
0.08 |
| B |
80≤s<90 |
35 |
y |
| C |
s<80 |
11 |
0.22 |
| 合 计 |
|
50 |
1 |
请根据上表提供的信息,解答下列问题:
(1)表中的x的值为 ,y的值为 。
(2)将本次参赛作品获得A等级的学生一次用A1,A2,A3,…表示,现该校决定从本次参赛作品中获得A等级学生中,随机抽取两名学生谈谈他们的参赛体会,请用树状图或列表法求恰好抽到学生A1和A2的概率。
某梁平特产专卖店销售“梁平柚”,已知“梁平柚”的进价为每个10元,现在的售价是每个16元,每天可卖出120个.市场调查反映:如调整价格,每涨价1元,每天要少卖出10个;每降价1元,每天可多卖出30个。
(1)如果专卖店每天要想获得770元的利润,且要尽可能的让利给顾客,那么售价应涨价多少元?
(2)请你帮专卖店老板算一算,如何定价才能使利润最大,并求出此时的最大利润?
如图,在正方形ABCD中,E、F分别为BC、AB上两点,且BE=BF,过点B作AE的垂线交AC于点G,过点G作CF的垂线交BC于点H延长线段AE、GH交于点M.
(1)求证:∠BFC=∠BEA;
(2)求证:AM=BG+GM。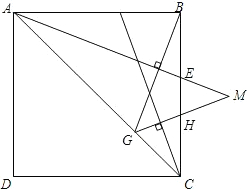
如图, 已知抛物线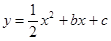 与y轴相交于C,与x轴相交于A、B,点A的坐标为(2,0),点C的坐标为(0,-1)。
与y轴相交于C,与x轴相交于A、B,点A的坐标为(2,0),点C的坐标为(0,-1)。
(1)求抛物线的解析式;
(2)点E是线段AC上一动点,过点E作DE⊥x轴于点D,连结DC,当△DCE的面积最大时,求点D的坐标;
(3)在直线BC上是否存在一点P,使△ACP为等腰三角形,若存在,求点P的坐标,若不存在,说明理由。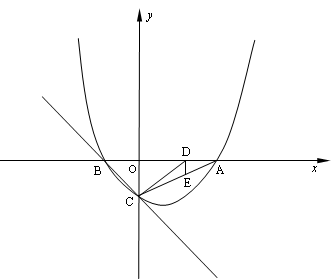
已知:把Rt△ABC和Rt△DEF按如图(1)摆放(点C与点E重合),点B、C(E)、F在同一条直线上.∠ACB = ∠EDF = 90°,∠DEF = 45°,AC =" 8" cm,BC =" 6" cm,EF =" 9" cm。
如图(2),△DEF从图(1)的位置出发,以1 cm/s的速度沿CB向△ABC匀速移动,在△DEF移动的同时,点P从△ABC的顶点B出发,以2 cm/s的速度沿BA向点A匀速移动。当△DEF的顶点D移动到AC边上时,△DEF停止移动,点P也随之停止移。DE与AC相交于点Q,连接PQ,设移动时间为t(s)(0<t<4.5)。解答下列问题:
(1)当t为何值时,点A在线段PQ的垂直平分线上?
(2)连接PE,设四边形APEC的面积为y(cm2),求y与t之间的函数关系式;是否存在某一时刻t,使面积y最小?若存在,求出y的最小值;若不存在,说明理由。
(3)是否存在某一时刻t,使P、Q、F三点在同一条直线上?若存在,求出此时t的值;若不存在,说明理由。(图(3)供同学们做题使用)
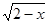 有意义,则x的取值范围( )。
有意义,则x的取值范围( )。




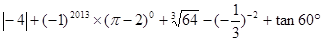
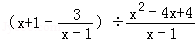 ,其中x满足方程:x2+x﹣6=0。
,其中x满足方程:x2+x﹣6=0。 粤公网安备 44130202000953号
粤公网安备 44130202000953号