安徽省望江县七年级第二学期期末质量检测数学
(9分)已知:△ABC是边长为4的等边三角形,点O在边AB上,⊙O过点B且
分别与边AB,BC相交于点D,E,EF⊥AC,垂足为F.
(1)求证:直线EF是⊙O的切线;
(2)当直线DF与⊙O相切时,求⊙O的半径.
(9分)如图1,在△ABC中,AB=AC,D是底边BC上的一点,BD>CD,将△ABC
沿AD剪开,拼成如图2的四边形ABDC′.
(1)四边形ABDC′具有什么特点?
(2)请同学们在图3中,用尺规作一个以MN,NP为邻边的四边形MNPQ,使四边形MNPQ具有上述特点(要求:写出作法,但不要求证明).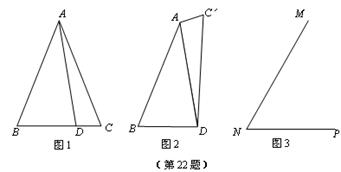
(9分)已知: ABCD的两边AB,AD的长是关于x的方程
ABCD的两边AB,AD的长是关于x的方程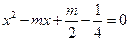 的两个实数根.
的两个实数根.
(1)当m为何值时,四边形ABCD是菱形?求出这时菱形的边长;
(2)若AB的长为2,那么 ABCD的周长是多少?
ABCD的周长是多少?
(9分)抛物线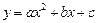 与y轴交于点
与y轴交于点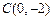 ,与直线
,与直线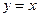
交于点 ,
,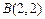 .
.
(1)求抛物线的解析式;
(2)如图,线段MN在线段AB上移动(点M与点A不重合,点N与点B不重合),且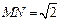 ,若M点的横坐标为m,过点M作
,若M点的横坐标为m,过点M作 x轴的垂线与x轴交于点P,过点N作x轴的垂线与抛物线交于点Q.以点P,M,Q,N为顶点的四边形能否为平行四边形?若能,请求出m的值;若不能,请说明理由.
x轴的垂线与x轴交于点P,过点N作x轴的垂线与抛物线交于点Q.以点P,M,Q,N为顶点的四边形能否为平行四边形?若能,请求出m的值;若不能,请说明理由.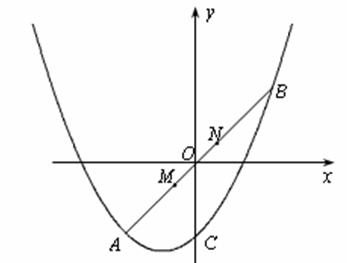
某车间5名工人日加工零件数分别为6,10,4,5,4,则这组数据的中位数是( )
| A.4 | B.5 |
| C.6 | D.10 |
将点A(2,1)向左平移2个单位长度得到点A′,则点A′的坐标是( )
| A.(0,1) | B.(2,﹣1) |
| C.(4,1) | D.(2,3) |
若a<c<0<b,则abc与0的大小关系是( )
| A.abc<0 | B.abc=0 |
| C.abc>0 | D.无法确定 |
下面的计算正确的是( )
| A.3x2•4x2=12x2 | B.x3•x5=x15 |
| C.x4÷x=x3 | D.(x5)2=x7 |
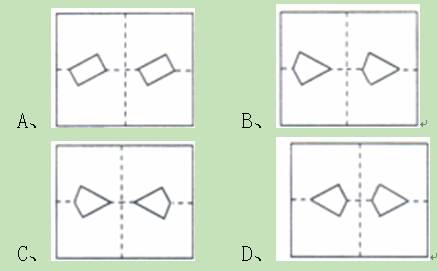
如图所示,将矩形纸片先沿虚线AB按箭头方向向右对折,接着对折后的纸片沿虚线CD向下对折,然后剪下一个小三角形,再将纸片打开,则打开后的展开图是( )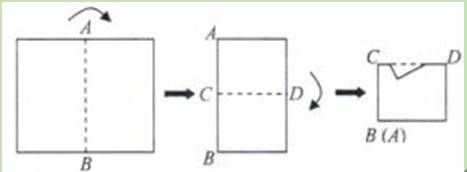
当实数x的取值使得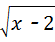 有意义时,函数y=4x+1中y的取值范围是( )
有意义时,函数y=4x+1中y的取值范围是( )
| A.y≥﹣7 | B.y≥9 |
| C.y>9 | D.y≤9 |
如图,AB切⊙O于点B,OA=2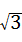 ,AB=3,弦BC∥OA,则劣弧BC的弧长为( )
,AB=3,弦BC∥OA,则劣弧BC的弧长为( )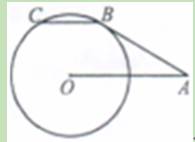
A.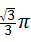 |
B.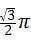 |
| C.π | D.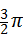 |
如图,以点O为位似中心,将五边形ABCDE放大后得到五边形A′B′C′D′E′,已知OA=10cm,OA′=20cm,则五边形ABCDE的周长与五边形A′B′C′D′E′的周长的比值是_________.
已知三条不同的直线a、b、c在同一平面内,下列四条命题:
①如果a∥b,a⊥c,那么b⊥c; ②如果b∥a,c∥a,那么b∥c;
③如果b⊥a,c⊥a,那么b⊥c;④如果b⊥a,c⊥a,那么b∥c.
其中真命题的是__________.(填写所有真命题的序号)
如图,AC是菱形ABCD的对角线,点E、F分别在边AB、AD上,且AE=AF.求证:△ACE≌△ACF.
如图,直线AB、CD、EF两两相交,则图中为同旁内角的角共有( )对。
A、3 B、4 C、5 D、6
如图所示,共有3个方格块,现在要把上面的方格块与下面的两个方格块合成一
个长方形的整体,则应将上面的方格块( )
| A.向右平移1格,向下3格 | B.向右平移1格,向下4格 |
| C.向右平移2格,向下4格 | D.向右平移2格,向下3格 |

把一张长方形的纸片按如图所示的方式折叠,EM、FM为折痕,折叠后的C点落
在B′M或B′M的延长线上,那么∠EMF的度数是( )
| A.85° | B.90° | C.95° | D.100° |

氢原子中电子和原子核之间最近距离为0.000 000 003 05厘米,用科学记数法表示为________________________厘米.
在一块长为a,宽为b的长方形草地上,有一条弯曲的柏油小路(小路任何地方
的水平宽度都是1个单位),则草地的面积为 。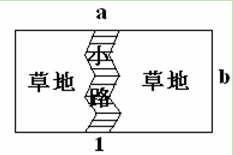
观察下列等式: ,
,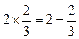 ,
, ,……
,……
(1)探索这些等式中的规律,直接写出第n个等式(用含n的等式表示)。
(2)试说明你的结论的正确性。
如图7,直线AB∥CD,直线EF分别交直线AB、CD于点E、F,FH平分∠EFD,若∠FEH=110º,求∠EHF的度数。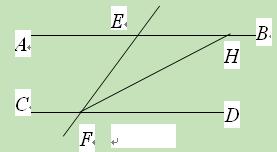
为了解七年级学生每周的课外阅读情况,某校语文组调查了该校七年级部分学生某周的课外阅读量(精确到千字),将调查数据经过统计整理后,得到如下频数分布直方图,回答下列问题:
(1)填空:
①该校语文组调查了 名学生的课外阅读量;
②左边第一组的频数= ,频率= 。
(2)求阅读量在1.1万字以上的人数。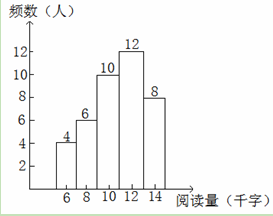
已知,AC⊥AB,EF⊥BC,AD⊥BC,∠1=∠2,请问AC⊥DG吗?请写出推理过程。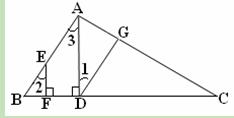
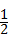 ,
,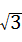 中为无理数的是( )
中为无理数的是( )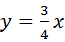
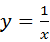
 的解是____________.
的解是____________. ,则12⊗(﹣1)=________
,则12⊗(﹣1)=________ .
.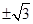
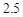
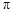
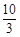
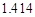
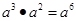
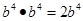
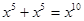
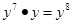
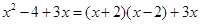
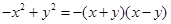
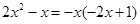
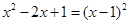
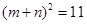 ,
,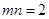 ,则
,则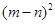 的值为( )
的值为( )
 ≥
≥
 的解集在数轴上表示正确的是( )
的解集在数轴上表示正确的是( )
 没有意义。
没有意义。
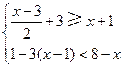 。
。 。
。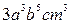 ,求它的高。
,求它的高。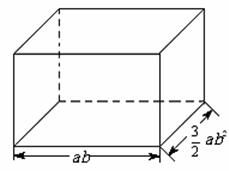
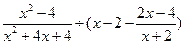 ,其中
,其中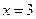 。
。 )
) 粤公网安备 44130202000953号
粤公网安备 44130202000953号