[福建]2014届福建省福州市九年级上学期期末质检数学试卷
某厂一月份的总产量为500吨,三月份的总产量达到为720吨.若平均每月增长率是 ,则可以列方程( )
,则可以列方程( )
A. |
B. |
C. |
D.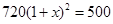 |
下列事件是随机事件的为( )
A.度量三角形的内角和,结果是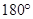 |
| B.经过城市中有交通信号灯的路口,遇到红灯 |
| C.爸爸的年龄比爷爷大 |
| D.通常加热到100℃时,水沸腾 |
将二次函数y=x2-2x+3化为y=(x-h)2+k的形式结果为 ( )
| A.y=(x+1)2+4 | B.y=(x-1)2+4 |
| C.y=(x+1)2+2 | D.y=(x-1)2+2 |
已知一个圆锥的侧面积是 ,母线为15,则这个圆锥的底面半径是 ( )
,母线为15,则这个圆锥的底面半径是 ( )
| A.5 | B.10 | C.15 | D.20 |
如图,CD是⊙O的直径,AB是弦(不是直径),AB⊥CD于点E,则下列结论正确的是( )
A.AE>BE B.
C.∠AEC=2∠D D.∠B=∠C.
根据下列表格对应值:
判断关于 的方程
的方程 的一个解
的一个解 的范围是( )
的范围是( )
A. <3.24 <3.24 |
B.3.24< <3.25 <3.25 |
C.3.25< <3.26 <3.26 |
D.3.25< <3.28 <3.28 |
如图,在矩形ABCD中,AB=1,AD=2,将AD绕点A顺时针旋转,当点D落在BC上点D′ 时,则CD′= .
如图在 的网格图(每个小正方形的边长均为1个单位长度)中,⊙A的半径为2个单位长度,⊙B的半径为1个单位长度,要使运动的⊙B与静止的⊙A内切,应将⊙B由图示位置向左平移 个单位长度.
的网格图(每个小正方形的边长均为1个单位长度)中,⊙A的半径为2个单位长度,⊙B的半径为1个单位长度,要使运动的⊙B与静止的⊙A内切,应将⊙B由图示位置向左平移 个单位长度.
如图,已知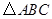 的三个顶点的坐标分别为
的三个顶点的坐标分别为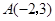 、
、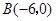 、
、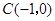 .
.
(1)请直接写出点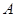 关于原点
关于原点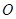 对称的点的坐标;
对称的点的坐标;
(2)将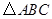 绕坐标原点
绕坐标原点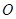 逆时针旋转90°.画出图形,直接写出点
逆时针旋转90°.画出图形,直接写出点 的对应点的坐标;
的对应点的坐标;
(3)请直接写出:以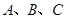 为顶点的平行四边形的第四个顶点
为顶点的平行四边形的第四个顶点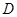 的坐标.
的坐标.
设点 的坐标(
的坐标(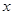 ,
, ),其中横坐标
),其中横坐标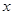 可取-1,2,纵坐标
可取-1,2,纵坐标 可取-1, 1,2,
可取-1, 1,2,
(1)求出点 的坐标的所有等可能结果(用树形图或列表法求解);
的坐标的所有等可能结果(用树形图或列表法求解);
(2)求点 与点
与点 (1,-1)关于原点对称的概率。
(1,-1)关于原点对称的概率。
如图,OC平分∠MON,点A在射线OC上,以点A为圆心,半径为2的⊙A与OM相切与点B,连接BA并延长交⊙A于点D,交ON于点E.
(1)求证:ON是⊙A的切线;
(2)若∠MON=60°,求图中阴影部分的面积.(结果保留π)
为了落实国务院的指示精神,某地方政府出台了一系列“三农”优惠政策,使农民收入大幅度增加.某农户生产经销一种农产品,已知这种产品的成本价为每千克20元,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)有如下关系:y=﹣2x+80.设这种产品每天的销售利润为w元.
(1)求w与x之间的函数关系式.
(2)该产品销售价定为每千克多少元时,每天的销售利润最大?最大利润是多少元?
(3)如果物价部门规定这种产品的销售价不高于每千克28元,该农户想要每天获得150元的销售利润,销售价应定为每千克多少元?
如图,点O是边长为1的等边△ABC内的任一点,设∠AOB=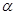 °,∠BOC=
°,∠BOC= °
°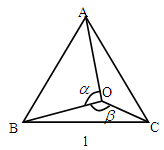
(1)将△BOC绕点C沿顺时针方向旋转60°得△ADC,连结OD,如图2所示. 求证:OD=OC。
(2)在(1)的基础上,将△ABC绕点C沿顺时针方向旋转60°得△EAC,连结DE,如图3所示. 求证:OA=DE
(3)在(2)的基础上, 当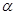 、
、 满足什么关系时,点B、O、D、E在同一直线上。并直接写出AO+BO+CO的最小值。
满足什么关系时,点B、O、D、E在同一直线上。并直接写出AO+BO+CO的最小值。
如图,在平面直角坐标系xOy中,将抛物线C1:y=x2+3先向右平移1个单位,再向下平移7个单位得到抛物线C2。C2的图象与x轴交于A、B两点(点A在点B的左侧)。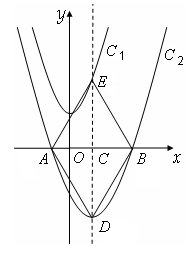
(1)求抛物线C2的解析式;
(2)若抛物线C2的对称轴与x轴交于点C,与抛物线C2交于点D,与抛物线C1交于点E,连结AD、DB、BE、EA,请证明四边形ADBE是菱形,并计算它的面积;
(3)若点F为对称轴DE上任意一点,在抛物线C2上是否存在这样的点G,使以O、B、F、G四点为顶点的四边形是平行四边形,如果存在,请求出点G的坐标,如果不存在,请说明理由。
 、
、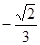 、
、 、
、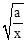 、
、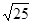 中,最简二次根式的个数是( )
中,最简二次根式的个数是( )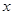 的一元二次方程
的一元二次方程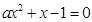 有实数根,则
有实数根,则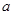 的取值范围是( )
的取值范围是( )
 且
且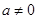
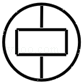



 向左平移2个单位,那么所得抛物线的表达式为( )
向左平移2个单位,那么所得抛物线的表达式为( )



 在实数范围内有意义,则
在实数范围内有意义,则 的取值范围是
的取值范围是 
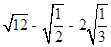
 粤公网安备 44130202000953号
粤公网安备 44130202000953号