河南省扶沟县初三下册28章《解直角三角形》检测题

下列各组图形有可能不相似的是(    ).

如图，D是⊿ABC的边AB上一点，在条件（1）△ACD＝∠B，（2）AC2＝AD·AB，（3）AB边上与点C距离相等的点D有两个，（4）∠B＝△ACB中，一定使⊿ABC∽⊿ACD的个数是

如图，∠ABD＝∠ACD，图中相似三角形的对数是（  ）

如图，在矩形ABCD中，点E是AD上任意一点，则有（  ）

已知两个相似三角形周长分别为8和6，则它们的面积比为（ ）。

A．4:3；

B．16:9；

C．2:；

D．。

两个相似三角形对应边之比是1:5，那么它们的周长比是（ ）。

A．；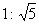

B．1:25；

C．1:5；

D．。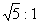

若⊿ABC∽⊿，∠A="40°," ∠B=110°,则∠=(   )
A. 40°          B110°        C70°        D30°

如图，在ΔABC中，AB=30，BC=24，CA=27，  AE=EF=FB，EG∥FD∥BC，FM∥EN∥AC，则图中阴影部分的三个三角形的周长之和为（    ）

A．70

B．75

C．81

D．80

如图，在△ABC中，△BAC＝90°，D是BC中点，AE∥AD交CB延长线于点E，则⊿BAE相似于______．

在一张比例尺为1：10000的地图上，我校的周长为18cm，则我校的实际周长为          。

如果两个相似三角形对应高的比为4：5，则这两个三角形的相似比是
，它们的面积的比是           。

三角形的三条边长分别为5cm，9cm，12cm，则连结各边中点所成三角形的周长为 ________cm。

△ABC中，∠ACB＝90°，CD是斜边AB上的高，AB＝4cm，AC＝cm，则AD＝________ cm。

在长8cm，宽6cm的矩形中，截去一个矩形，使留下的矩形与原矩形相似，那么留下的矩形面积是_______cm2

如图，由边长为1的25个小正方形网格上有一个与⊿ABC相似且面积最大的⊿A1B1C1，使它的三个顶点都落在小正方形的顶点上，则⊿A1B1C1的面积为___________

如图，这是圆桌正上方的灯泡（看作一个点）发出的光线照射桌面后，在地上形成阴影（圆形 ）的示意图，已知桌面的直径为1.2米，桌面距地面1米，灯泡距地面3米，则地上阴影部分的面积是______.             

如图，点C、D在线段AB上，⊿PCD是等边三角形．

（1）当AC、CD、DB满足怎样的关系时，⊿ACP∽⊿PDB？
（2）当⊿ACP∽⊿PDB时，求⊿APB的度数．

如图，BD、CE为⊿ABC的高，求证⊿AED＝⊿ACB．

已知矩形ABCD中，E为DC的中点，连接BE，AF⊥BE于点F，AB＝10cm，BC＝12cm，求AF长。

在Rt△ABC中，，，，则∠A的度数为（  ）。

如图，在梯形ABCD中，AD∥BC，AC⊥AB，AD=CD，cos∠DCA=，BC=10，则AB的值是（  ）

在高为h的山顶上，测得山脚一建筑物的顶端与底部的俯角分别为30°、60°，那么建筑物的高度是（  ）。

A．h

B．h

C．h

D．h

如图，从山顶A望地面上的C、D两点，测得它们的俯角分别是45°和30°，已知CD=100m，D、C、B在同一直线上，则山高AB=（  ）

A、100m         B、50m        C、50m        D、50(＋1)m

如图，在Rt△ABC中，CD是斜边AB的中线，已知CD=2，AC=3，则sinB的值是（  ）。

A．

B．

C．

D．

王芳同学从A地沿北偏西60°方向走100m到B地，再从B地向正南方向走200m到C地，此时王芳同学离A地（  ）。

如图，在Rt△ABC中，∠ACB=90°，CD⊥AB，cos∠BCD=，BD=1，则边AB的长度是（  ）。

A．

B．

C．2

D．

如图，已知一商场自动扶梯的长l为10米，该自动扶梯到达的高度h为6米，自动扶梯与地面所成的角为α，则tanα的值为（  ）。

A．

B．

C．

D．

如图，在一次龙卷风中，一棵大树在离地面若干米处折断倒下，B为折断处最高点，树顶A落在距树根C 12m处，测得∠BAC=48°，则原树高约   m。(保留两位小数)

如图，根据所示图形中所给的数据求得CD高度约为       m。(≈1.73，计算结果保留整数)

如图，在Rt△ABC中，∠C=90°，AM是BC边上的中线，sin∠CAM=，则tan∠B的值为     。

已知是α锐角，且sin (α－10°)= ，则α=     。

在直角梯形ABCD中，AD∥BC，∠ABC=90°，∠C =60°，AD=DC=2，则BC=       。

有一拦水坝的横断面是等腰梯形，它的上底为6米，下底长10米，高2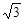米，那么此拦水坝斜坡度为       ，坡角为        。

计算。（10＇）
（1）2cos30°－tan60°＋tan45° 
（2）2sin60°－3tan30°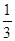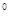＋ ()＋(-1)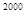  

如图，在Rt△ABC中，∠C=90°，CD⊥AB于D，已知sinA=，BD=2，求BC的长。

如图，在矩形ABCD中，E是BC边上的点，AE=BC，DF⊥AE，垂足为F，连接DE，

　（1）求证：△ABE≌△DFA。
（2）如果AD＝10，AB＝6，求sin∠EDF的值。

如图，小明在楼上点A处观察旗杆BC，测得旗杆顶部B的仰角为30°，测得旗杆底部C的俯角为60°，已知点A距地面高AD为12m，求旗杆的高度。（12＇）

如图，A、B是两座现代化城市，C是一个古城遗址，C城在A城的北偏东30°方向，在B城的北偏西45°方向，且C城与A城相距120千米，B城在A城的正东方向，以C为圆心，以60千米为半径的圆形区域内有古迹和地下文物，现要在A、B两城市间修建一条笔直的高速公路，（14＇）

（1）请你计算公路的长度。（结果保留根号）
（2）请你分析这条公路有没有可能是对古迹或文物赞成损毁。