[江苏]2012-2013学年江苏扬州广陵区八年级下期中考试数学试卷
已知反比例函数y=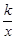 的图象过点P(1,-3),则反比例函数图象位于( )
的图象过点P(1,-3),则反比例函数图象位于( )
| A.第一、二象限 | B.第一、三象限 |
| C.第二、四象限 | D.第三、四象限 |
反比例函数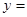
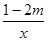 (
(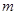 为常数)当
为常数)当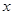 <0时,
<0时,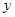 随
随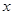 的增大而增大,则
的增大而增大,则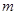 的取值范围是( )
的取值范围是( )
A.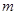 <0 <0 |
B.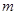 < <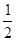 |
C.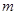 > >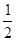 |
D.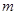 ≥ ≥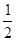 |
将 中的
中的 都变为原来的4倍,则分式的值( )
都变为原来的4倍,则分式的值( )
| A.不变 | B.是原来的4倍 | C.是原来的16倍 | D.是原来的8倍 |
如图,直线y=mx与双曲线y= 交于A、B两点,过点A作AM⊥x轴,垂足为M,连结BM,若
交于A、B两点,过点A作AM⊥x轴,垂足为M,连结BM,若 =3,则k的值是( )
=3,则k的值是( )
A.3 B、m-3 C、m D、6
要使函数y=(2m-3)x+(3-m)的图像经过第一、二、三象限,则m的取值范围是___ _____.
如图所示,点B是反比例函数y= 图象上一点,过点B分别作x轴、y轴的垂线,如果构成的矩形面积是4,那么反比例函数的解析式是 _______ ______
图象上一点,过点B分别作x轴、y轴的垂线,如果构成的矩形面积是4,那么反比例函数的解析式是 _______ ______
34个同学到某地春游,用200元钱去买快餐,每人一份。该地的快餐有两种,6元一份和5元一份。如果你是生活委员,6元一份的最多能买 份。
已知 与
与 -2成反比例,且当
-2成反比例,且当 =4时,
=4时, =5, 求:
=5, 求:
(1) 与
与 之间的函数关系式;
之间的函数关系式;
(2)当 时,求
时,求 的值.
的值.
甲种商品每件价格比乙种商品多5元,用90元买得甲种商品的件数与用60元买得乙种商品的件数相等,求甲、乙两商品每件价格各是多少元?
课堂上,李老师出了这样一道题:已知x=2013,求代数式 的值。小明觉得直接代入计算太繁了,请你来帮他解决,并写出具体过程。
的值。小明觉得直接代入计算太繁了,请你来帮他解决,并写出具体过程。
如图,已知A(4,a),B(-2,-4)是一次函数y=k x+b 的图象和反比例函数 的图象的交点.
的图象的交点.
(1)求反比例函数和一次函数的解析式;
(2)求△AOB的面积.
(3)根据图象求出使一次函数的值大于反比例函数的值时,x的取值范围.
为执行中央“节能减排,美化环境,建设美丽新农村” 的国策,我市某村计划建造A、B两种型号的沼气池共20个,以解决该村所有农户的燃 料问题.两种型号沼
气池的占地面积、使用农户数及造价见下表:
| 型号 |
占地面积 (单位:m2/个) |
使用农户数 (单位:户/个) |
造价 (单位:万元/个) |
| A |
15 |
18 |
2 |
| B |
20 |
30 |
3 |
已知可供建造沼气池的占地面积不超过370m2,该村农户共有498户.
(1)满足条件的方案共有哪几种?写出解答过程.
(2)通过计算判断,哪种建造方案最省钱?造价最低是多少万元?
 有意义,则x的取值范围是( )
有意义,则x的取值范围是( )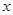 >-3
>-3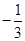
 ,下列不等式中不正确的是( )
,下列不等式中不正确的是( )



 和
和 的图像可能是( )
的图像可能是( ) 
 = 时,分 式
= 时,分 式 值为0.
值为0. 时,分式
时,分式 的值为 .
的值为 . 与
与 的最简公分母是__ __。
的最简公分母是__ __。 的分式方程
的分式方程 有增根,则
有增根,则 .
. 的图象同时过A
的图象同时过A 、B
、B 、C
、C 三点,则将
三点,则将 、
、 、
、 表示的三个数用“<”连接是
表示的三个数用“<”连接是  的值为整数的整数x的值 是 。
的值为整数的整数x的值 是 。 无解,则a的范围为
无解,则a的范围为 
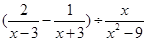 (2)
(2) 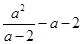

 (2)
(2)
 的图象交于点A(3,2).
的图象交于点A(3,2).
 粤公网安备 44130202000953号
粤公网安备 44130202000953号