[江苏]2012-2013学年江苏省扬州市广陵区七年级下学期期中考试数学试卷
下面计算结果正确的是:( )
| A.(-3)0=1; | B.a3+a3=a6; |
C.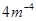 = =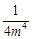 ; ; |
D.(xy2)3=xy6 |
如图,下列能判定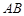 ∥
∥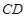 的条件有( )个.
的条件有( )个.
(1)  ;(2)
;(2)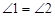 ;(3)
;(3) 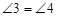 ;(4)
;(4) 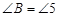 .
.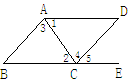
| A.1 | B.2 | C.3 | D.4 |
判断下列说法正确的是( )
| A.平移前后图形的形状和大小都没有发生改变 |
| B.三角形的三条高都在三角形的内部 |
| C.两条直线被第三条直线所截,同旁内角互补 |
| D.三角形的一条角平分线将三角形分成面积相等的两部分 |
如果100x2-kxy+9y2是一个完全平方式,那么k的值为( )
| A.30 | B.60 | C.±30 | D.±60 |
如图是赛车跑道的一部分路段,已知AB∥CD,则 ∠A=110°, ∠E=80°则∠D的度数为( )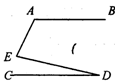
| A.40° | B.30° | C.20° | D.10° |
如图,从边长为(a+4)cm的正方形纸片中剪去一个边长为(a+1)cm的正方形(a>0),剩余部分沿虚线又剪拼成一个矩形(不重叠无缝隙),则矩形的面积为
| A.(2a2+5a)cm2 | B.(6a+15) cm2 |
| C.(6a+9)cm2 | D.(3a+15) cm2 |
四个电子宠物排座位,一开始,鼠、猴、虎、猫分别坐在1、2、3、4号座位上,以后不停地变换位置,第一次上下两行交换,第二次是在第一次换位后,再左右两列交换位置,第三次再上下两行交换,第四次再左右两列交换……这样一直下去,则第2013次交换位置后,老虎所在的号位是 ( )
在五边形ABCDE中,∠A=100°, ∠B=∠C=112°, ∠D=108°则∠E=____°
如图,AD、AE分别是△ABC的角平分线和高,∠B=60°,∠C=70°,则∠EAD= °
如图所示,已知△ ABC中,∠A=84°,点B、C、M在一条直线上,∠ABC和∠ACM两角的平分线交于点P1,∠P1BC和∠P1CM两角的平分线交于点P2,∠P2BC和∠P2CM两角的平分线交于点P3,则∠P3=_____°。
如图,在正方形网格上有一个△ABC.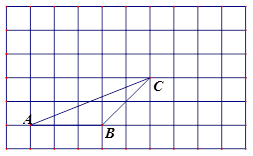
(1)把△ABC沿水平方向向右平移4小方格得到△A’B’C’
(2)在△ABC中作AB边上的高CD和BC边上的中线AE;
(3)若网格上的最小正方形边长为1,求△ABC的面积.
如图,某市有一块长为(3a+b)米,宽为(2a+b)米的长方形地块,规划部门计划将阴影部分进行绿化,中间将修建一座雕像,则绿化的面积是多少平方米?(用含a、b的代数式表示)并求出当a=3,b=2时的绿化面积.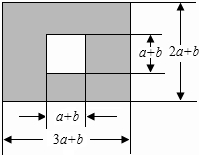
如图 ,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥A B,垂足为F. 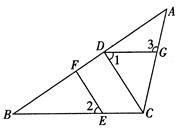
(1)CD与EF平行吗?为什么?
(2 )如果∠1=∠2,且∠3=115°,求∠ACB的度数.
将幂的运算逆向思维可以得到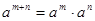 ,
,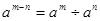 ,
,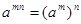 ,
,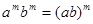 ,在解题过程中,根据算式的结构特征,逆向运用幂的运算法则,常可化繁为简,化难为易,使问题巧妙获解,收到事半功倍的效果如:
,在解题过程中,根据算式的结构特征,逆向运用幂的运算法则,常可化繁为简,化难为易,使问题巧妙获解,收到事半功倍的效果如:
(1)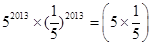 =__________
=__________
(2) 若3×9m×27m=311,则m的值为____________.
(3) 比较大小:,则a、b、c、d的大小关系是____________
(提示:如果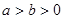 ,n为正整数,那么
,n为正整数,那么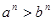 )
)
如图①所示是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的方式拼成一个正方形.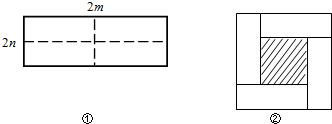
(1)图②中的阴影部分的正方形的边长等于_________(用含m、n的代数式表示);
(2)请用两种不同的方法列代数式表示图②中阴影部分的面积.
方法①_____________________.方法②____________________;
(3)观察图②,试写出(m+n)2,(m-n)2,mn这三个代数式之间的等量关系
__________________________________________________________________
(4)根据(3)题中的等量关系,解决如下问题:若a+b=6,ab=4,求(a-b)2的值.

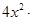 □=
□=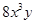 ,则“□”中应填入的代数式是 。
,则“□”中应填入的代数式是 。



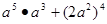
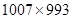 (2) 先化简再求值:
(2) 先化简再求值: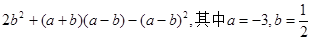
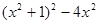
 粤公网安备 44130202000953号
粤公网安备 44130202000953号