2013年初中数学单元提优测试卷-平面图形的认识
给出以下判断:(1)线段的中点是线段的重心
(2)三角形的三条中线交于一点,这一点就是三角形的重心
(3)平行四边形的重心是它的两条对角线的交点
(4)三角形的重心是它的中线的一个三等分点
那么以上判断中正确的有( )
| A.一个 | B.两个 | C.三个 | D.四个 |
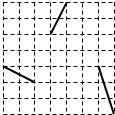
已知在正方形网格中,每个小方格都是边长为1的正方形,A,B两点在小方格的顶点上,位置如图所示,点C也在小方格的顶点上,且以A,B,C为顶点的三角形面积为1,则点C的个数为( )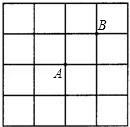
| A.3个 | B.4个 | C.5个 | D.6个 |
把一张形状是多边形的纸片剪去其中某一个角,剩下的部分是一个四边形,则这张纸片原来的形状不可能是( )
| A.六边形 | B.五边形 | C.四边形 | D.三角形 |
已知三角形的两边a=3,b=7,第三边是c,且a<b<c,则c的取值范围是( )
| A.4<c<7 | B.7<c<10 | C.4<c<10 | D.7<c<13 |
某人在广场上练习驾驶汽车,两次拐弯后,行驶方向与原来相同,这两次拐弯的角度可能是( )
| A.第一次左拐30°,第二次右拐30° |
| B.第一次右拐50°,第二次左拐130° |
| C.第一次右拐50°,第二次右拐130° |
| D.第一次向左拐50°,第二次向左拐120° |
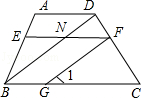
如图所示,AB∥EF∥DC,EG∥DB,则图中与∠1相等的角(∠1除外)共有( )
| A.6个 | B.5个 | C.4个 | D.2个 |
某城市有四条直线型主干道分别为l1,l2,l3,l4,l3和l4相交,l1和l2相互平行且与l3、l4相交成如图所示的图形,则共可得同旁内角( )对.
| A.4 | B.8 | C.12 | D.16 |
如果两个角的两边分别平行,而其中一个角比另一个角的4倍少30°,那么这两个角是( )
| A.42°、138° | B.都是10° |
| C.42°、138°或42°、10° | D.以上都不对 |
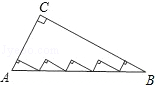
如图,若干全等正五边形排成环状.图中所示的是前3个五边形,要完成这一圆环还需( )个五边形.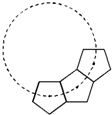
| A.6 | B.7 | C.8 | D.9 |
在如图所示的单位正方形网格中,将△ABC向右平移3个单位后得到△A′B′C′(其中A、B、C的对应点分别为A′、B′、C′),则∠BA′A的度数是 度.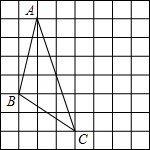
图中正方形GFCD和正方形AEHG的边长都是整数,它们的面积之和是117,P是AE上一点,Q是CD上一点.则三角形BCH的面积是 ;四边形PHQG的面积是 .
图1是一个三角形,分别连接这个三角形三边的中点得到图2;再分别连接图2中间小三角形的中点,得到图3. (若三角形中含有其它三角形则不记入)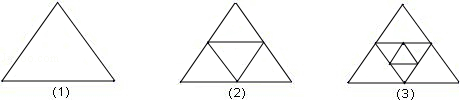
(1)图2有 个三角形;图3中有 个三角形
(2)按上面方法继续下去,第20个图有 个三角形;第n个图中有 个三角形.(用n的代数式表示结论)
如图,在△ABC中,∠ACB=60°,∠BAC=75°,AD⊥BC于D,BE⊥AC于E,AD与BE交于H,则∠CHD= .
如图,四边形ABCD的对角线AC和BD相交于O点,如果S△ABD=5,S△ABC=6,S△BCD=10,那么S△OBC .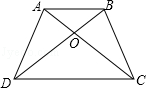
在△ABC中,∠A=47°,高BE、CF所在直线交于点O,且点E、F不与点B、C重合,则∠BOC= .
探索:在图1至图3中,已知△ABC的面积为a,
(1)如图1,延长△ABC的边BC到点D,使CD=BC,连接DA.若△ACD的面积为S1,则S1= (用含a的代数式表示)
(2)如图2,延长△ABC的边BC到点D,延长边CA到点E,使CD=BC,AE=CA,连接DE.若△DEC的面积为S2,则S2= (用含a的代数式表示)
(3)在图2的基础上延长AB到点F,使BF=AB,连接FD,FE,得到△DEF(如图3).若阴影部分的面积为S3,则S3= (用含a的代数式表示),并运用上述(2)的结论写出理由.
发现:像上面那样,将△ABC各边均顺次延长一倍,连接所得端点,得到△DEF(如图3),此时,我们称△ABC向外扩展了一次.可以发现,扩展一次后得到的△DEF的面积是原来△ABC面积的 倍.
应用:要在一块足够大的空地上栽种花卉,工程人员进行了如下的图案设计:首先在△ABC的空地上种红花,然后将△ABC向外扩展三次(图4已给出了前两次扩展的图案).在第一次扩展区域内种谎话,第二次扩展区域内种紫花,第三次扩展区域内种蓝花.如果种红花的区域(即△ABC)的面积是10平方米,请你运用上述结论求出:
①种紫花的区域的面积;
②种蓝花的区域的面积.
(1)如图1,已知∠1=∠2,∠B=∠C,可推得AB∥CD,理由如下:
∵∠1=∠2(已知),
且∠1=∠CGD( ),
∴∠2=∠CGD(等量代换)
∴CE∥BF( )
∴∠ ECD =∠BFD( )
又∵∠B=∠C(已知)
∴∠BFD=∠B( )
∴AB∥CD( ).
(2)已知,如图2,AD∥BE,∠1=∠2,∠A与∠E相等吗?试说明理由.
过A、B、C、D、E五个点中任意三点画三角形;
(1)其中以AB为一边可以画出 个三角形;
(2)其中以C为顶点可以画出 个三角形.
如图,用剪刀沿直线剪去五边形的一个角得到一个新的五边形,你能想出剪去一个角的其它方法吗?在图(2)(3)中画出示意图,并回答剪去一个角后剩下的是几边形?并求出剪后得到的多边形的内角和.
如图,在长为50米,宽为30米的长方形地块上,有纵横交错的几条小路,宽均为1米,其它部分均种植花草.试求出种植花草的面积是多少?






 粤公网安备 44130202000953号
粤公网安备 44130202000953号