2012年北师大版初中数学九年级下3.2圆的对称性练习卷
圆既是轴对称图形,又是_________对称图形,它的对称轴是_______, 对称中心是____。
来源:2012年北师大版初中数学九年级下3.2圆的对称性练习题
如图,⊙O的直径为10,弦AB=8,P是弦AB上的一个动点,那么OP长的取值范围是_____.
来源:2012年北师大版初中数学九年级下3.2圆的对称性练习题
已知:如图,有一圆弧形拱桥,拱的跨度AB=16cm,拱高CD=4cm,那么拱形的半径是____m.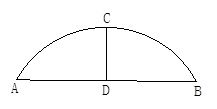
来源:2012年北师大版初中数学九年级下3.2圆的对称性练习题
如图,D、E分别是⊙O的半径OA、OB上的点,CD⊥OA,CE⊥OB,CD=" CE," 则 与
与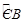 弧长的大小关系是_________.
弧长的大小关系是_________.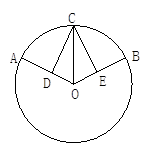
来源:2012年北师大版初中数学九年级下3.2圆的对称性练习题
如图,在⊙O中,AB、AC是互相垂直且相等的两条弦,OD⊥AB,OE⊥AC,垂足分别为D、E,若AC=2cm,则⊙O的半径为_____cm.
来源:2012年北师大版初中数学九年级下3.2圆的对称性练习题
如图,在半径为2cm的⊙O中有长为2 cm的弦AB,则弦AB所对的圆心角的度数为( )
cm的弦AB,则弦AB所对的圆心角的度数为( )
| A.60° | B.90° | C.120° | D.150° |
来源:2012年北师大版初中数学九年级下3.2圆的对称性练习题
如图,⊙O的直径为10cm,弦AB为8cm,P是弦AB上一点,若OP的长为整数, 则满足条件的点P有( )
| A.2个 | B.3个 | C.4个 | D.5个 |
来源:2012年北师大版初中数学九年级下3.2圆的对称性练习题
如图,A是半径为5的⊙O内一点,且OA=3,过点A且长小于8的弦有( )
| A.0条 | B.1条 | C.2条 | D.4条 |
来源:2012年北师大版初中数学九年级下3.2圆的对称性练习题
如图,AB是⊙O的弦(非直径),C、D是AB上两点,并且AC=BD.试判断OC与OD 的数量关系并说明理由.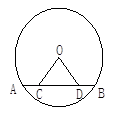
来源:2012年北师大版初中数学九年级下3.2圆的对称性练习题
如图,⊙O表示一圆形工件,AB=15cm,OM=8cm,并且MB:MA="1:4," 求工件半径的长.
来源:2012年北师大版初中数学九年级下3.2圆的对称性练习题
已知:如图,在⊙O中,弦AB的长是半径OA的 倍,C为
倍,C为 的中点,AB、OC 相交于点M.试判断四边形OACB的形状,并说明理由.
的中点,AB、OC 相交于点M.试判断四边形OACB的形状,并说明理由.
来源:2012年北师大版初中数学九年级下3.2圆的对称性练习题
如图,AB是⊙O的直径,P是AB上一点,C、D分别是圆上的点,且∠CPB=∠DPB, ,试比较线段PC、PD的大小关系.
,试比较线段PC、PD的大小关系.
来源:2012年北师大版初中数学九年级下3.2圆的对称性练习题
在半径为5cm的⊙O中,弦AB的长等于6cm,若弦AB的两个端点A、B在⊙O上滑动(滑动过程中AB的长度不变),请说明弦AB的中点C在滑运过程中所经过的路线是什么图形.
来源:2012年北师大版初中数学九年级下3.2圆的对称性练习题
 的中点,P是直径MN上一动点.⊙O的半径为1,问P在直线MN上什么位置时,AP+BP的值最小?并求出AP+BP的最小值.
的中点,P是直径MN上一动点.⊙O的半径为1,问P在直线MN上什么位置时,AP+BP的值最小?并求出AP+BP的最小值.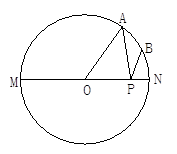
 粤公网安备 44130202000953号
粤公网安备 44130202000953号