2011届上海市卢湾区初三上学期期末第一次模拟数学卷
已知∠AOB=30°,自∠AOB顶点O引射线OC,若∠AOC :∠AOB="4" :3 ,那么∠BOC的度数是
| A.10° | B.40° | C.70° | D.10°或70° |
“某幼儿园给小朋友分苹果,若每个小朋友分3个则剩1个;若每个小朋友分4个则少2个,问苹果有多少个?” 若设共有x个苹果,则列出的方程是
A. |
B. |
C. |
D. |
如图,边长为(m+2)的正方形纸片剪出一个边长为m的正方形之后,剩余部分又剪拼成一个矩形(不重叠无缝隙),若拼成的矩形一边长为2,则另一边长是 ▲ .(用含m的代数式表示)
如下图,是由一些大小相同的小正方体组合成的简单几何体

(1)图中有 块小正方体;
(2)该几何体的主视图如图所示,请在下面方格纸中分别画出它的左视图和俯视图.
下列各小题中,都有OE平分∠AOC,OF平分∠BOC.

(1)如图①, 若OA在∠BOC的外部,则∠AOB与∠EOF的数量关系是:∠AOB= ∠EOF.
(2)如图②,若OA在∠BOC的内部,则题(1)中的数量关系是否仍成立?若成立,
请说明理由.
如果两个相似三角形对应边之比是1∶4,那么它们的对应中线之比是…( ).
| A.1∶2; | B.1∶4; | C.1∶8; | D.1∶16. |
抛物线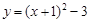 的顶点坐标是………………………………………( ).
的顶点坐标是………………………………………( ).
| A.(1,3); | B.(1,– 3); | C.(–1 ,3); | D.(– 1,–3). |
已知点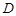 、
、 分别在
分别在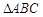 的边
的边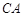 、
、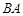 的延长线上,
的延长线上, ∥
∥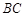 ,
,
若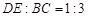 ,则向量
,则向量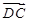 等于……………………………………( ).
等于……………………………………( ).
A.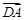 ; ; |
B. ; ; |
C.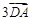 ; ; |
D.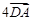 . . |
如图,已知在平行四边形 中,
中, ,
, ,
, .
.
(1)用 、
、 表示
表示 、
、 ;(直接写出答案)
;(直接写出答案)
(2)求作 分别在
分别在 、
、 方向上的分向量.
方向上的分向量.
(不要求写作法,但要指出图中表示结论的向量)
如图,一块梯形木料 ,
, ∥
∥ ,经测量知
,经测量知 cm,
cm, cm,
cm, ,
, ,求梯形木料
,求梯形木料 的高.
的高.
(备用数据 :sin 67.4° = ,cos 67.4° = ,tan 67.4° = )
:sin 67.4° = ,cos 67.4° = ,tan 67.4° = )
已知抛物线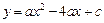 与
与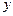 轴交于点
轴交于点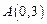 ,点
,点 是抛物线上的点,且满足
是抛物线上的点,且满足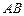 ∥
∥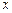 轴,点
轴,点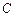 是抛物线的顶点.
是抛物线的顶点.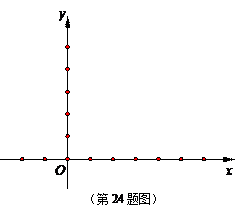
(1)求抛物线的对称轴及 点坐标;
点坐标;
(2)若抛物线经过点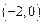 ,求抛物线的表达式;
,求抛物线的表达式;
(3)对(2)中的抛物线,点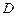 在线段
在线段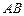 上,若以点
上,若以点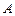 、
、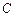 、
、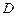 为顶点的三角形与
为顶点的三角形与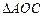 相似,试求点
相似,试求点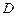 的坐标.
的坐标.
如图,已知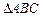 与
与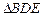 都是等边三角形,点
都是等边三角形,点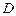 在边
在边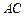 上(不与
上(不与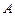 、
、 重合),
重合), 与
与 相交于点
相交于点 .
.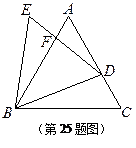
(1)求证:
 ∽
∽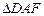 ;
;
(2)若 ,设
,设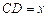 ,
,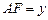 ;
;
①求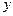 关于
关于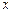
 的函数解析式及定义域;
的函数解析式及定义域;
②当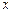 为何值时,
为何值时,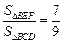 ?
?
以坐标原点为圆心,1为半径的圆分别交x,y轴的正半轴于点A,B.
(1)如图一,动点P从点A处出发,沿x轴向右匀速运动,与此同时,动点Q从点B处出发,沿圆周按顺时针方向匀速运动.若点Q的运动速度比点P的运动速度慢,经过1秒后点P运动到点(2,0),此时PQ恰好是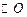 的切线,连接OQ. 求
的切线,连接OQ. 求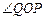 的大小;
的大小;
(2)若点Q按照(1)中的方向和速度继续运动,点P停留在点(2,0)处不动,求点Q再经过5秒后直线PQ被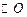 截得的弦长
截得的弦长

 、
、 在数轴上的位置如图所示,则化简
在数轴上的位置如图所示,则化简 的结果为
的结果为



 …+
…+ 的值,可令
的值,可令 …
… ,则
,则 …
… ,因此
,因此 ,所以
,所以 .仿照以上推理计算出
.仿照以上推理计算出 …
… 的值是
的值是



 的相反数是___▲______;
的相反数是___▲______; 的倒数是____▲_______
的倒数是____▲_______ = ▲ ;合并同类项:
= ▲ ;合并同类项: ▲
▲ 的次数是 ▲;若
的次数是 ▲;若 与
与 是同类项,则
是同类项,则 _▲_
_▲_ 的解为 ▲ ;若
的解为 ▲ ;若 ,则
,则 = ▲
= ▲

 的方程
的方程 的解是
的解是 ,则
,则 的值是 ▲
的值是 ▲
 个图中所贴剪纸“○”的个数为 ▲
个图中所贴剪纸“○”的个数为 ▲ 
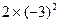

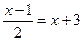
 的方程2- =0和方程2
的方程2- =0和方程2
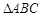 中,∠C=90º,若AB=4,
中,∠C=90º,若AB=4,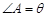 ,则AC的长为……………( ).
,则AC的长为……………( ).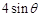 ;
;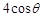 ;
; ;
;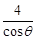
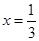 的是…………………………………………( ).
的是…………………………………………( ).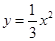 ;
;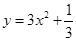 ;
;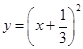 ;
;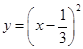
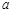 、
、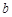 、
、 、
、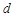 满足
满足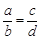 ,那么下列等式不一定成立的是………( ).
,那么下列等式不一定成立的是………( ).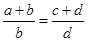 ;
;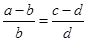 ;
; ;
;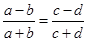
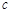 是线段
是线段 和线段
和线段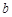 的比例中项,若
的比例中项,若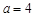 ,
,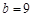 ,则线段
,则线段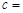 _______
_______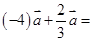 ________
________ 在
在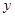 轴右侧的部分是 (填“上升”或“下降”)
轴右侧的部分是 (填“上升”或“下降”) 平移,使平移后的抛物线顶点坐标为
平移,使平移后的抛物线顶点坐标为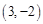 ,那么平移后的抛物线的表达式为_____
,那么平移后的抛物线的表达式为_____ 中,
中,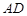 ∥
∥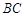 ,点
,点 在
在 上,点
上,点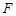 在
在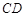 上,
上, 是中位线,若
是中位线,若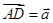 ,
,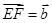 ,则用
,则用 、
、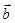 表示
表示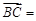 _______
_______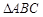 中,
中,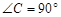 ,
, 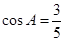 ,则
,则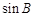 =
=  中,
中, ,如果
,如果 ,
, ,那么
,那么
 、
、 分别是
分别是 的边
的边 、
、 上的点,
上的点, ,
, ,
, ,如果要使
,如果要使 ∥
∥ ,则
,则
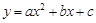 与
与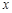 轴交于点
轴交于点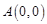 、
、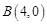 ,则抛物线的对称轴为直线
,则抛物线的对称轴为直线 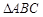 中,
中, ,
,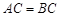 ,若点
,若点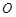 是
是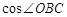 =_______
=_______ 沿直线
沿直线 翻折,使点
翻折,使点 与
与 边上的点
边上的点 重合,若
重合,若 ,
, ,则
,则

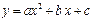 经过点(–5,0)、(–1,0)、(1,12),求这个抛物线的表达式及其顶点坐标
经过点(–5,0)、(–1,0)、(1,12),求这个抛物线的表达式及其顶点坐标 中,
中, ,点
,点 在
在 上,
上, ,
, ,
,  ,求
,求 的长.
的长.
 中,
中, 与
与 相交于点
相交于点 ,AB⊥AC,CD⊥BD.
,AB⊥AC,CD⊥BD.
 ∽
∽ ;
; ,
, ,求
,求 的值
的值 ,则此坡面的坡角是________
,则此坡面的坡角是________ 粤公网安备 44130202000953号
粤公网安备 44130202000953号