[江苏]2007年初中毕业升学考试(江苏泰州卷)数学
下列说法正确的是( )
| A.小红和其他四个同学抽签决定从星期一到星期五的值日次序,她第三个抽签,抽到星期一的概率比前两个人小 |
| B.某种彩票中奖率为10%,小王同学买了10张彩票,一定有1张中奖 |
| C.为了了解一批炮弹的杀伤半径,应进行普查 |
| D.晚会前,班长对全班同学爱吃哪几种水果作了民意调查,最终买什么水果由众数决定 |
如图,王大伯家屋后有一块长12m,宽8m的矩形空地,他在以长边 为直径的半圆内种菜,他家养的一只羊平时拴在
为直径的半圆内种菜,他家养的一只羊平时拴在 处的一棵树上,为了不让羊吃到菜,拴羊的绳长可以选用( )
处的一棵树上,为了不让羊吃到菜,拴羊的绳长可以选用( )
| A.3m | B.5m | C.7m | D.9m |
2008年奥运会日益临近,某厂经授权生产的奥运纪念品深受人们欢迎,今年1月份以来,该产品原有库存量为 (
( )的情况下,日销量与产量持平,3月底以来需求量增加,在生产能力不变的情况下,该产品一度脱销,下图能大致表示今年1月份以来库存量
)的情况下,日销量与产量持平,3月底以来需求量增加,在生产能力不变的情况下,该产品一度脱销,下图能大致表示今年1月份以来库存量 与时间
与时间 之间函数关系的是( )
之间函数关系的是( )
现有甲、乙、丙、丁、戊五个同学,他们分别来自一中、二中、三中.已知:(1)每所学校至少有他们中的一名学生;(2)在二中联欢会上,甲、乙、戊作为被邀请的客人演奏了小提琴;(3)乙过去曾在三中学习,后来转学了,现在同丁在同一个班学习;(4)丁、戊是同一所学校的三好学生.根据以上叙述可以断定甲所在的学校为( )
| A.一中 | B.二中 | C.三中 | D.不确定 |
已知:二次函数 ,下列说法错误的是( )
,下列说法错误的是( )
A.当 时, 时, 随 随 的增大而减小 的增大而减小 |
B.若图象与 轴有交点,则 轴有交点,则 |
C.当 时,不等式 时,不等式 的解集是 的解集是 |
D.若将图象向上平移1个单位,再向左平移3个单位后过点 ,则 ,则 |
我国城镇居民2004年人均收入为9422元,2006年为11759元,假设这两年内人均收入平均年增长率相同,则年增长率为 (精确到0.1%).
如图,在 的正方形格纸中,有一个以格点为顶点的
的正方形格纸中,有一个以格点为顶点的 ,请你找出格纸中所有与
,请你找出格纸中所有与 成轴对称且也以格点为顶点的三角形,这样的三角形共有 个.
成轴对称且也以格点为顶点的三角形,这样的三角形共有 个.
数学课上,年轻的刘老师在讲授“轴对称”时,设计了如下四种教学方法:
①教师讲,学生听;
②教师让学生自己做;
③教师引导学生画图,发现规律;
④教师让学生对折纸,观察发现规律,然后画图.
数学教研组长将上述教学方法作为调研内容发到全年级8个班420名同学手中,要求每位同学选出自己最喜欢的一种,他随机抽取了60名学生的调查问卷,统计如图:
(1)请将条形统计图补充完整,并计算扇形统计图中方法③的圆心角.
(2)全年级同学中最喜欢的教学方法是哪一种?选择这种教学方法的约有多少人?
(3)假如抽取的60名学生集中在某两个班,这个调查结果还合理吗?为什么?
(4)请你对老师的教学方法提出一条合理化的建议.
2007年5月17日我市荣获“国家卫生城市称号”.在“创卫”过程中,要在东西方向 两地之间修建一条道路.已知:如图
两地之间修建一条道路.已知:如图 点周围180m范围内为文物保护区,在
点周围180m范围内为文物保护区,在 上点
上点 处测得
处测得 在
在 的北偏东
的北偏东 方向上,从
方向上,从 向东走500m到达
向东走500m到达 处,测得
处,测得 在
在 的北偏西
的北偏西 方向上.
方向上.
(1) 是否穿过文物保护区?为什么?(参考数据:
是否穿过文物保护区?为什么?(参考数据: )
)
(2)若修路工程顺利进行,要使修路工程比原计划提前5天完成,需将原定的工作效率提高25%,则原计划完成这项工程需要多少天?
某学校七年级数学兴趣小组组织一次数学活动.在一座有三道环形路的数字迷宫的每个进口处都标记着一个数,要求进入者把自己当做数“1”,进入时必须乘进口处的数,并将结果带到下一个进口,依次累乘下去,在通过最后一个进口时,只有乘积是5的倍数,才可以进入迷宫中心,现让一名5岁小朋友小军从最外环任一个进口进入.
(1)小军能进入迷宫中心的概率是多少?请画出树状图进行说明.
(2)小组两位组员小张和小李商量做一个小游戏,以猜测小军进迷宫的结果比胜负.游戏规则规完:小军如果能进入迷宫中心,小张和小李各得1分;小军如果不能进入迷宫中心,则他在最后一个进口处所得乘积是奇数时,小张得3分,所得乘积是偶数时,小李得3分,你认为这个游戏公平吗?如果公平,请说明理由;如果不公平,请在第二道环进口处的两个数中改变其中一个数使游戏公平.
(3)在(2)的游戏规则下,让小军从最外环进口任意进入10次,最终小张和小李的总得分之和不超过28分,请问小军至少几次进入迷宫中心?
通过市场调查,一段时间内某地区某一种农副产品的需求数量 (千克)与市场价格
(千克)与市场价格 (元/千克)(
(元/千克)( )存在下列关系:
)存在下列关系:
 (元/千克) (元/千克) |
5 |
10 |
15 |
20 |
 (千克) (千克) |
4500 |
4000 |
3500 |
3000 |
又假设该地区这种农副产品在这段时间内的生产数量 (千克)与市场价格
(千克)与市场价格 (元/千克)成正比例关系:
(元/千克)成正比例关系: (
( ).现不计其它因素影响,如果需求数量
).现不计其它因素影响,如果需求数量 等于生产数量
等于生产数量 ,那么此时市场处于平衡状态.
,那么此时市场处于平衡状态.
(1)请通过描点画图探究 与
与 之间的函数关系,并求出函数关系式;
之间的函数关系,并求出函数关系式;
(2)根据以上市场调查,请你分析:当市场处于平衡状态时,该地区这种农副产品的市场价格与这段时间内农民的总销售收入各是多少?
(3)如果该地区农民对这种农副产品进行精加工,此时生产数量 与市场价格
与市场价格 的函数关系发生改变,而需求数量
的函数关系发生改变,而需求数量 与市场价格
与市场价格 的函数关系未发生变化,那么当市场处于平衡状态时,该地区农民的总销售收入比未精加工市场平衡时增加了17600元.请问这时该农副产品的市场价格为多少元?
的函数关系未发生变化,那么当市场处于平衡状态时,该地区农民的总销售收入比未精加工市场平衡时增加了17600元.请问这时该农副产品的市场价格为多少元?
如图①, 中,
中, ,
, .它的顶点
.它的顶点 的坐标为
的坐标为 ,顶点
,顶点 的坐标为
的坐标为 ,
, ,点
,点 从点
从点 出发,沿
出发,沿 的方向匀速运动,同时点
的方向匀速运动,同时点 从点
从点 出发,沿
出发,沿 轴正方向以相同速度运动,当点
轴正方向以相同速度运动,当点 到达点
到达点 时,两点同时停止运动,设运动的时间为
时,两点同时停止运动,设运动的时间为 秒.
秒.
(1)求 的度数.
的度数.
(2)当点 在
在 上运动时,
上运动时, 的面积
的面积 (平方单位)与时间
(平方单位)与时间 (秒)之间的函数图象为抛物线的一部分,(如图②),求点
(秒)之间的函数图象为抛物线的一部分,(如图②),求点 的运动速度.
的运动速度.
(3)求(2)中面积 与时间
与时间 之间的函数关系式及面积
之间的函数关系式及面积 取最大值时点
取最大值时点 的坐标.
的坐标.
(4)如果点 保持(2)中的速度不变,那么点
保持(2)中的速度不变,那么点 沿
沿 边运动时,
边运动时, 的大小随着时间
的大小随着时间 的增大而增大;沿着
的增大而增大;沿着 边运动时,
边运动时, 的大小随着时间
的大小随着时间 的增大而减小,当点
的增大而减小,当点 沿这两边运动时,使
沿这两边运动时,使 的点
的点 有几个?请说明理由.
有几个?请说明理由.
 的倒数是( )
的倒数是( )






 随的增大而减小的是( )
随的增大而减小的是( )

 (
( )
) (
( )
)
 ,
, ,以
,以 为位似中心,按比例尺
为位似中心,按比例尺 ,把
,把 缩小,则点
缩小,则点 的对应点
的对应点 的坐标为( )
的坐标为( )
 或
或
 或
或
 中,自变量
中,自变量 的取值范围是( )
的取值范围是( )



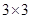 方格中的规律,在下面4个符号中选择一个填入方格左上方的空格内( )
方格中的规律,在下面4个符号中选择一个填入方格左上方的空格内( )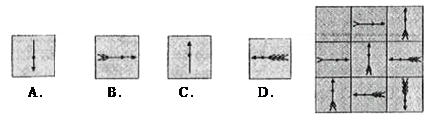
 ,
, ,
, ,
, 的方差
的方差 .
. ,直线
,直线 与
与 轴围成图形的周长是 (结果保留根号).
轴围成图形的周长是 (结果保留根号). 中,
中, ,
, ,
, ,
, ,
, ,将腰
,将腰 以点
以点 为中心逆时针旋转
为中心逆时针旋转 至
至 ,连结
,连结 ,则
,则 的面积是 .
的面积是 .
 的扇形做成一个圆锥模型的侧面,则此圆锥的高为 cm(结果保留根号).
的扇形做成一个圆锥模型的侧面,则此圆锥的高为 cm(结果保留根号). .
. ,其中,
,其中, 是方程
是方程 的根.
的根. 中,点
中,点 ,
, 分别是
分别是 的中点,
的中点, 分别是
分别是 的中点,
的中点, 满足什么条件时,四边形
满足什么条件时,四边形 是菱形?请证明你的结论.
是菱形?请证明你的结论.
 中,
中, ,点
,点 为
为 的中点,以
的中点,以 为直径的
为直径的 切
切 于点
于点 ,
, .
.
 的长;(2)过点
的长;(2)过点 交
交 ,求
,求 的长.
的长. 粤公网安备 44130202000953号
粤公网安备 44130202000953号