[安徽]2011-2012学年度安徽省芜湖市七年级数学下学期期末数学试卷

下列各组长度的线段为边，能构成三角形的是（　　　）

如图，在一张透明的纸上画一条直线，在外任取一点Q并折出过点Q且与垂直的直线。这样的直线能折出(     )

已知点M(3a-9，1-a)在x轴上，则a=(    )

若＜，则一定满足（   ）

A．＞0

B．＜0

C．≥0

D．≤0

△ABC中,∠A=∠B=∠C,则△ABC是(     )
 

商店出售下列形状的地砖：①正方形；②长方形；③正五边形；＠正六边形．若只选购其中某一种地砖镶嵌地面，可供选择的地砖共有．（    ）

用代入法解方程组 有以下步骤：
①：由⑴，得 ⑶   ②：把⑶代入⑴，得
③：整理得  3=3   ④：∴可取一切有理数，原方程组有无数个解
以上解法，造成错误的一步是(      )

地理老师介绍到：长江比黄河长836千米，黄河长度的6倍比长江长度的5倍多
1284千米，小东根据地理教师的介绍，设长江长为x千米，黄河长为y千米，然后通过列、
解二元一次方程组，正确的求出了长江和黄河的长度，那么小东列的方程组可能是（      ）

A．

B．

C．

D．

正n边形的内角和等于1080⁰，则n＝　　　。

如图④，AB∥CD，∠BAE = 120º，∠DCE = 30º，则∠AEC =           度。
      

已知三角形的三边之长分别为3，6，a，则a的取值范围是______________.

请写出一个在第一象限内且到两坐标轴的距离都相等的点的坐标____________.

某次数学测验中共有16道题目，评分办法：答对一道得6分，答错一道扣2分，不答得0分．某学生有一道题未答，那么这个同学至少要答对______道题，成绩才能在60分以上

阅读下列语句：
①对顶角相等；②同位角相等；③画∠AOB的平分线OC；④这个角等于30°吗？在这些语句中，属于真命题的是_____ _____(填写序号)

已知关于的二元一次方程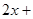 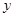=7中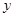，的系数已经模糊不清，但已知是这个方程的解，那么原方程是_________  _______。

某市为了了解该市6万名七年级学生的身体素质情况，随机抽取了500名七年级学生进行检测，身体素质达标率为92％.这次检测的样本容量是____  _______。

解方程组                                             

解不等式组，并把不等式组的解集在数轴上表示出来。

x取哪些非负整数时,的值大于与1的差 。

已知关于x、y的方程组的解都是正数，求m的取值范围；

如图：已知AB∥DE∥CF，若∠ABC=70°，∠CDE=130°，求∠BCD的度数。

如图，方格纸中每个小方格都是边长为1个单位长度的正方形，在建立平面直角坐标系后，⊿ABC的顶点在格点上。 且A（1，-4），B（5，-4），C（4，-1）
画出⊿ABC；
求出⊿ABC 的面积；
若把⊿ABC向上平移2个单位长度，再向左平移4个单位长度得到⊿BC，在图中画出⊿BC，并写出B的坐标。

北京举办2008年夏季奥运会以来，奥运知识在我国不断传播，小刚就本班学生的对奥运知识的了解程度进行了一次调查统计．A：熟悉，B：了解较多，C：一般了解．图1和图2是他采集数据后，绘制的两幅不完整的统计图，请你根据图中提供的信息解答以下问题：
求该班共有多少名学生；
在条形图中，将表示“一般了解”的部分补充完整．
在扇形统计图中，计算出“了解较多”部分所对应的圆心角的度数；
如果全年级共1000名同学，请你估算全年级对奥运知识 “了解较多”的学生人数．

某汽车租赁公司要购买轿车和面包车共辆．其中面包车不能超过轿车的两倍，轿车每辆万元，面包车每辆万元，公司可投入的购车款不超过61万元．
符合公司要求的购买方案有哪几种？请说明理由．
如果每辆轿车的日租金为元，每辆面包车的日租金为元．假设新购买的这辆车每日都可租出，要使这辆车的日租金收入不低于1600元，那么应选择以上哪种购买方案？

图1，线段AB、CD相交于点O,连接AD、CB，我们把形如图1的图形称之为“8字形”.如图2，在图1的条件下，∠DAB和∠BCD的平分线AP和CP相交于点P，并且与CD、AB分别相交于M、N.试解答下列问题：
在图1中，请直接写出∠A、∠B、∠C、∠D之间的数量关系：                ；
    
仔细观察，在图2中“8字形”的个数：      个；
图2中，当∠D=50度，∠B=40度时，求∠P的度数。
图2中∠D和∠B为任意角时，其他条件不变，试问∠P与∠D、∠B之间存在着怎样的数量关系.说明理由。（直接写出结果，不必证明）。