[广东]2011—2012学年广东省湛江市八年级上学期第一次月考数学试卷
在△ABC和△DEF中,已知∠C=∠D,∠B=∠E要判定这两个三角形全等,还需条件( )
| A.AB=ED | B.AB=FD | C.AC=FD | D.∠A=∠E |
如图2,如果直线m是多边形ABCDE的对称轴,其中∠A=110°,∠B=130°那么∠BCD的度数等于( )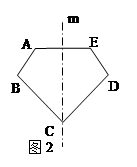
| A.50° | B.60° | C.70° | D.80° |
平面内与A、B、C(不在同一直线上)三点等距离的点( )
A、没有 B、只有1个 C、有2个 D、有4个
下列条件,不能使两个三角形全等的条件是( )
| A.两边一角对应相等 | B.两角一边对应相等 |
| C.三边对应相等 | D.两边和它们的夹角对应相等 |
如图3,M是∠AOB的平分线上的一点, MD⊥OA于D,ME⊥OB于E,下列结论中不正确的是( )
| A.MD=ME | B.OD="OE" |
| C.∠OMD=∠ OME, | D.OM=MD+ME |
等腰三角形的两边分别为5和10,则它的周长是 ( )
| A.20 | B.15 | C.25 | D.20或25 |
如图4,△ABC中,AB="AC" ∠A=30°DE垂直平分AC,则∠DCB的度数为( )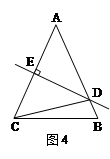
| A.80° | B.75° | C.65° | D.45° |
如图5,△ABC中,∠ABC,∠ACB的平分线相交于O,MN过点O是与BC平行,△ABC的周长为20,△AMN的周长为12,则BC的长为( )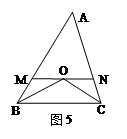
| A.8 | B.4 | C.32 | D.16 |
如图6,△ABC中,AB=AC,AD⊥BC于D,点E,F在BC上,BE=CF,则图中全等三角形 的对数共有( )
| A.2时 | B.3对 | C.4对 | D.5对 |
若△DEF是由△ABC经过3次轴对称变换得到的,△ABC的面积是6,则△DEF的面积是 。
在△ABC和△DEF中,∠A=∠D,AC=DF,要使△ABC≌△DEF,则需要补充的条件是 (写一个即可)
已知△ABC与△A′B′C′关于y轴对称,点A的坐标为(1,3),则点A的对应点A′的坐标是 。
如图8,在△ABC中,∠CAB=120°,∠B=∠C=30°,AB、AC的垂直平分线分别交BC于E、F,则∠EAF= 。
如图9,△ABC中,∠C=90°,AD平分∠BAC,若AB=5、CD=2,则△ABD的面积是 。
如图10,小明上午在理发店理发时,从镜子内看到背后普通时钟的时针与分针的位置如图所示,此时时间是 。
下图是按一定规律摆放的图案,按此规律,第2011个图案与第1~4个图案中相同的是 (只填数字)
如图11,△ABC三个顶点的坐标分别为A(-3,-1)、B(-4,-3)C(-2,-5)
在图中作出△ABC关于x轴对称的图形;
在图中作出△ABC关于y轴对称的图形;
求S△ABC。
如图14,一艘轮船以15海里/时的速度由南向北航行,在A处测得小岛P在北偏西15°方向上,两小时后,轮船在B处测得小岛P在北偏西30°方向上.在小岛周围18海里内有暗礁,若轮船不改变方向仍继续向前航行,问:有无触礁的危险?并说明你的理由.
如图15,在△ABC中,D是BC的中点,DE⊥AB,DF⊥AC,垂直分别是E、F,BE=CF。
图中有几对全等三角形?请一一列出。
选择一对全等的三角形进行证明
如图15,AB=2,BC=5,AB⊥BC与B,l⊥BC于C,点P自点B开始沿射线BC移动,过点P作PQ⊥PA交直线l于点Q。
求证:∠A=∠QPC
当点P运动到何处时,PA=PQ?并说明理由。





 粤公网安备 44130202000953号
粤公网安备 44130202000953号