[福建]2011-2012学年福建省泉州市八年级下期期末模拟考试(一)数学卷
下列说法正确的是( )
| A.非负实数就是指一切正数 |
| B.数轴上任意一点都对应一个有理数 |
C.若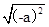 是实数,则a为任意实数 是实数,则a为任意实数 |
| D.若|a|= -a,则a<0 |
已知正比例函数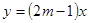 的图象上两点A(x1,y1),B(x2,y2),当
的图象上两点A(x1,y1),B(x2,y2),当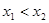 时,有
时,有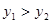 ,则m的取值范围是( )
,则m的取值范围是( )
A.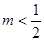 |
B.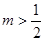 |
C.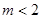 |
D. |
已知ab<0,点P(a、b)在反比例函数 的图象上,则直线y=ax+b不经过( )
的图象上,则直线y=ax+b不经过( )
| A.第一象限 | B.第二象限 |
| C.第三象限 | D.第四象限 |
点P是x轴正半轴上的一个动点,过点P作 x轴的垂线PQ交双曲线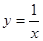 于点Q,连结OQ,当点P沿x轴正半轴方向运动时,Rt△QOP面积( )
于点Q,连结OQ,当点P沿x轴正半轴方向运动时,Rt△QOP面积( )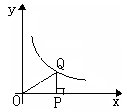
| A.逐渐增大 | B.逐渐减小 |
| C.保持不变 | D.无法确定 |
在Rt△ABC中,∠C=90 ,若sinA=
,若sinA=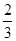 ,那么tanB等于( )
,那么tanB等于( )
A.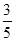 |
B.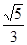 |
C.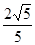 |
D.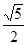 |
如图,在△ABC中,P为AB上一点,在下列四个条件中①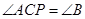 ②
②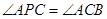 ,③
,③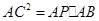 ,
,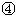
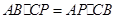 ,其中能满足△APC∽△ACB的是( )
,其中能满足△APC∽△ACB的是( )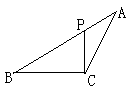
A.①② |
B.①③ |
C.②③ |
D.①②③ |
每周一学校都要举行庄严的升国旗仪式,让我们体会到了国旗的神圣。某同学产生了用所学知识测量旗杆高度的想法。在地面距杆脚5米的地方,他利用测倾器测得杆顶的仰角为α,且tanα=3,则杆高(不计测倾器的高度)为( )
| A.10m | B.12m | C.15m | D.20m |
甲乙两人在相同条件下,各打靶5次,环数如下:甲:6、8、9、9、8;乙:10、7、7、7、9,则甲乙两人射击成绩( )
| A.甲比乙稳定 | B.乙比甲稳定 |
| C.甲乙相同 | D.无法比较 |
如图所示,棋盘上有A、B、C三个黑子与P、Q两个白子,要使△ABC∽△RPQ,则第三个白子R应放的位置可以是( )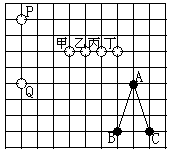
(A)甲 (B)乙 (C)丙 (D)丁
某音像社对外出租光盘的收费方法是:每张光盘出租的头两天每天收费0.8元,以后每天收0.5元,那么一张光盘在出租的第n天(n是大于2的自然数)应收租金是 元。
盒子中有红球和白球各2个,小玲把球从盒子中一个一个地摸出来,则红球和白球相间出现(可以是“红白红白”也可以是“白红白红”)的机会是 。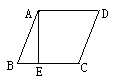
已知:如图,在△ABC中,∠ACB= 900, CD⊥AB,垂足是D,BC=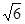 ,BD=1。求CD,AD的长。
,BD=1。求CD,AD的长。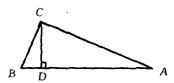
如图,Rt△ABO的顶点A是双曲线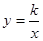 与直线
与直线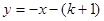 在第二象限的交点,AB⊥
在第二象限的交点,AB⊥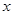 轴于B,且
轴于B,且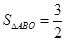 。求这两个函数的解析式。
。求这两个函数的解析式。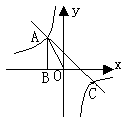
小明和小亮用如图所示的两个转盘做游戏,转动两个转盘各一次。若两次数字和为奇数,则小明得1分;而若和为偶数,则小亮得1分。这个游戏对双方公平吗?为什么?(请用列表法说明理由)。如果不公平,如何修改规则,使游戏对双方都公平。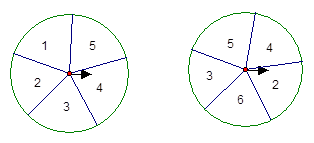
机动车出发前油箱内有油42升,行驶若干小时后,途中在加油站加油若干升,油箱中余油量Q(升)与行驶时间t(时)之间的函数关系如图所示,根据图回答问题: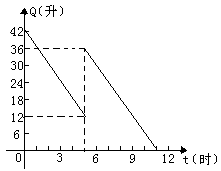
(1)机动车行驶__ _小时后加油;
(2)加油前油箱余油量Q与行驶时间t之间的函数关系式是_ ,中途加油_____升;
(3)如果加油站距目的地还有230千米,车速为40千米/时,要达到目的地,油箱中的油是否够用?请说明理由?
已知平面直角坐标系上有6个点:A(3,3),B(1,1),C(9,1),D(5,3),E(-1,-9),F(-2,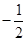 ),请将上述的6个点按下列的要求分成两类,并写出同类点具有而另一类点不具有的一个特征(请将答案按下列要求写在横线上:特征不能用否定形式表述,点用字母表示。)①甲类含两个点,乙类含其余四个点
),请将上述的6个点按下列的要求分成两类,并写出同类点具有而另一类点不具有的一个特征(请将答案按下列要求写在横线上:特征不能用否定形式表述,点用字母表示。)①甲类含两个点,乙类含其余四个点
甲类:点 、 是同一类点,其特征是 ;乙类:点 、 、 、 是同一类点,其特征是 。
②甲类含三个点,乙类含其余三个点
甲类:点 、 、 是同一类点,其特征是 ;乙类:点 、 、 是同一类点,其特征是 。
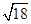 是同类二次根式的是( )
是同类二次根式的是( )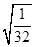
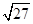
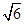
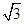
 。
。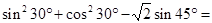 。
。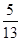 ,则这个菱形的面积是 。
,则这个菱形的面积是 。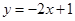 的图象上,则a和b的大小关系是 。
的图象上,则a和b的大小关系是 。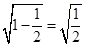 ,
,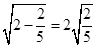 ,
,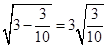 ,
,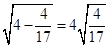 ,按上述规律,第n个等式是 。
,按上述规律,第n个等式是 。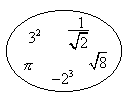
 粤公网安备 44130202000953号
粤公网安备 44130202000953号