[广东]2011-2012学年广东省惠州市惠城区十一校九年级上学期期末联考数学卷
自上海世博会开幕以来,中国馆以其独特的造型吸引了世人的目光.据预测,在会展期间,参观中国馆的人次数估计可达到14 900 000,此数用科学记数法表示是 ( ) 
A. |
B. |
C. |
D. |
如图所示,AB、AC切⊙O于B、C两点,∠A=50°,点P是圆上异于B、C的一动点,则∠BPC的度数是 ( )

A 65° B 115° C 65°或115° D 130°或50°
|
如图,Rt△ABC中,∠ACB=90°,DE过点C,且DE∥AB,若∠ACD=50°,则∠B的度数是 
若: ,
,
…,观察前面计算过程,寻找计算规律计算 (直接写出计算结果),并比较
(直接写出计算结果),并比较 (填“
(填“ ”或“
”或“ ”或“=”)
”或“=”)
如图,正方形网格中的每一个小正方形的边长都是1,四边形ABCD的四个顶点都在格点上,O为AD边的中点,若把四边形ABCD绕着点O顺时针旋转90°,试解决下列问题:
(1)画出四边形ABCD旋转后的图形;
(2)求点C旋转过程中所经过的路径长.
市区某楼盘准备以每平方米7000元的均价对外销售,由于国务院有关房地产的
新政策出台后,购房者持币观望.为了加快资金周转,房地产开发商对价格经过两
次下调后,决定以每平方米5670元的均价开盘销售.求平均每次下调的百分率;
如图,两个大小不同的等腰直角三角形三角板如图甲所示放置,图乙是由它抽象出的几何图开,B,C,E在同一条直线上,连结DC。请找出图乙中的全等三角形,并给予证明(说明,结论中不得含有未标识的字母)
如图已知E、F分别是□ABCD的边BC、AD上的点,且BE=DF.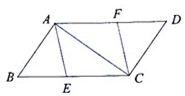
(1) 求证:四边形AECF是平行四边形;
(2) 若BC=10,∠BAC=90°,且四边形AECF是菱形,求BE的长 .
将如图所示的牌面数字分别是1,2,3,4的四张扑克牌背面朝上,洗匀后放在桌面上.
(1)从中随机抽出一张牌,牌面数字是偶数的概率是 ;
(2)从中随机抽出二张牌,两张牌牌面数字的和是5的概率是 ;
(3)先从中随机抽出一张牌,将牌面数字作为十位上的数字,然后将该牌放回并重新洗匀,再随机抽取一张,将牌面数字作为个位上的数字,请用画树状图或列表的方法求组成的两位数恰好是4的倍数的概率.
正比例函数y=k1x的图象与反比例函数 (x>0)的图象交于点M(a,1),MN⊥x轴于点N(如图),若△OMN的面积等于2,求这两个函数的解式
(x>0)的图象交于点M(a,1),MN⊥x轴于点N(如图),若△OMN的面积等于2,求这两个函数的解式
如图,已知直线 交⊙O于A、B两点,AE是⊙O的直径,点C为⊙O 上一点,过C作
交⊙O于A、B两点,AE是⊙O的直径,点C为⊙O 上一点,过C作 ,垂足为D。问:当AC满足什么条件时,CD为⊙O的切线,请说明理由。
,垂足为D。问:当AC满足什么条件时,CD为⊙O的切线,请说明理由。
李晖到“宇泉牌”服装专卖店做社会调查.了解到商店为了激励营业员的工作积极性,实行“月总收入=基本工资+计件奖金”的方法,并获得如下信息:
| 营业员 |
小俐 |
小花 |
| 月销售件数(件) |
200 |
150 |
| 月总收入(元) |
1400 |
1250 |
假设月销售件数为 件,月总收入为
件,月总收入为 元,销售每件奖励
元,销售每件奖励 元,营业员月基本工资为
元,营业员月基本工资为 元.
元.
(1)求 的值;
的值;
(2)若营业员小俐某月总收入不低于 元,那么小俐当月至少要卖服装多少件?
元,那么小俐当月至少要卖服装多少件?
一动点沿着数轴向右平移3个单位,再向左平移2个单位,相当于向右平移1
个单位.用实数加法表示为 3+( )=1.若坐标平面上的点作如下平移:沿x轴方向平移的数量为a(向右为正,向左为负,平移
)=1.若坐标平面上的点作如下平移:沿x轴方向平移的数量为a(向右为正,向左为负,平移 个单位),沿y轴方向平移的数量为b(向上为正,向下为负,平移
个单位),沿y轴方向平移的数量为b(向上为正,向下为负,平移 个单位),则把有序数对{a,b}叫做这一平移的“平移量”;“平移量”{a,b}与“平移量”{c,d}的加法运算法则为
个单位),则把有序数对{a,b}叫做这一平移的“平移量”;“平移量”{a,b}与“平移量”{c,d}的加法运算法则为  .
.
(1)计算:{3,1}+{1,2};
(2)动点P从坐标原点O出发,先按照“平移量”{3,1}平移到A,再按照“平移量”{1,2}平移到B;若先把动点P按照“平移量”{1,2}平移到C,再按照“平移量”{3,1}平移,最后的位置还是点O吗? 在图1中画出四边形OABC.
(3)如图2,一艘船从码头O出发,先航行到湖心岛码头P(2,3),再从码头P航行到码头Q(5,5),最后回到出发点O. 请用“平移量”加法算式表示它的航行过程.
 的相反数是( )
的相反数是( )







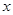 时,二次根式
时,二次根式  在实数范围内有意义
在实数范围内有意义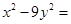 _______________.
_______________.


 粤公网安备 44130202000953号
粤公网安备 44130202000953号