江苏省江阴市华士片九年级5月调研考试数学试卷
若双曲线 过点(2,6),则该双曲线一定过点( )
过点(2,6),则该双曲线一定过点( )
| A.(―3,―4) | B.(4,―3) | C.(―6,2) | D.(4,4) |
某班抽取6名同学参加体能测试,成绩如下:80,90,75, 75,80,80,下列表述错误( )
| A.众数是80 | B.中位数是75 | C.平均数是80 | D.方差是 |
若一个正多边形的一个外角是40°,则这个正多边形的边数是( )
| A.10 | B.9 | C.8 | D.6 |
方程x2-2x= -2实数根的情况是( )
-2实数根的情况是( )
| A.有三个实数根 | B.有两个实数根 |
| C.有一个实数根 | D.无实数根 |
如图,已知扇形的圆心角为 (定值),半径为
(定值),半径为 (定值),分别在图一、二中作扇形的内接矩形,若按图一作出的矩形面积的最大值为
(定值),分别在图一、二中作扇形的内接矩形,若按图一作出的矩形面积的最大值为 ,则按图二作出的矩形面积的最大值为( )
,则按图二作出的矩形面积的最大值为( )
A. |
B. |
C. |
D. |
据媒体报道,我国因环境污染造成的巨大经济损失,每年高达680000000元,这个数用科学记数法表示为 元.
如图,直线 分别与
分别与 轴、
轴、 轴交于A、B两点,点P是
轴交于A、B两点,点P是
 的图像上一点,PH⊥
的图像上一点,PH⊥ 轴于H,当以P为圆心,PH为半径的圆与直线AB相切时,OH的长为 .
轴于H,当以P为圆心,PH为半径的圆与直线AB相切时,OH的长为 .
如图,正方形ABCD中,AB=2,动点E从点A出发向点D运动,同时动点F从点D出发向点C运动,点E、F运动的速度相同,当它们到达各自终点时停止运动,运动过程中线段AF、BE相交于点P,M是线段BC上任意一点,则MD+MP的最小值为 .
如图,在 ABCD中,点E在边BC上,点F在BC的延长线上,且BE=CF.
ABCD中,点E在边BC上,点F在BC的延长线上,且BE=CF.
求证:∠BAE=∠CDF.
根据小明和小丽的对话解答下列问题:
(小明友情提醒:可借助画树状图或列表的方法,列举所有等可能的结果,再进行计算.
小丽友情提醒:情况可不唯一哦.)
某市对九年级学生进行了一次学业水平测试,成绩评定分A、B、C、D四个等第.为了解这次数学测试成绩情况,相关部门从该市的农村、县镇、城市三类群体的学生中共抽取2 000名学生的数学成绩进行统计分析,相应数据的统计图表如下:

(1)请将上面表格中缺少的三个数据补充完整;
(2)若该市九年级共有60 000名学生参加测试,试估计该市学生成绩合格以上(含合格)的人数.
如图是某通道的侧面示意图,已知AB∥CD∥EF,AM∥BC∥DE,AB=CD=EF,∠AMF=90°,∠BAM=30°,AB=6m.
(1)求FM的长;
(2)连接AF,若sin∠FAM= ,求AM的长.
,求AM的长.
一棉花种植区的农民研制出采摘棉花的单人便携式采棉机,采摘效率高,能耗低,绿色环保.经测试,一个人操作该采棉机的采摘效率为35公斤/时,大约是一个人手工采摘的3.5倍,购买一台采棉机需900元.雇人采摘棉花,按每采摘1公斤棉花 元的标准支付雇工工资,雇工每天工作8小时.
元的标准支付雇工工资,雇工每天工作8小时.
(1)一个雇工手工采摘棉花,一天能采摘多少公斤?
(2)一个雇工手工采摘棉花7.5天获得的全部工钱正好购买一台采棉机,求a的值;
(3)在(2)的前提下,种植棉花的专业户张家和王家均雇人采摘棉花,王家雇用的人数是张家的2倍.张家雇人手工采摘,王家所雇的人中有 的人自带采棉机采摘,
的人自带采棉机采摘, 的人手工采摘.两家采摘完毕,采摘的天数刚好一样,张家付给雇工工钱总额为14400元.王家这次采摘棉花的总重量是多少?
的人手工采摘.两家采摘完毕,采摘的天数刚好一样,张家付给雇工工钱总额为14400元.王家这次采摘棉花的总重量是多少?
某中学九年级学生步行到郊外春游.一班的学生组成前队,速度为4 km/h,二班的学生组成后队,速度为6 km/h.前队出发1 h后,后队才出发,同时,后队派一名联络员骑自行车在两队之间不间断地来回进行联络,他骑车的速度为12 km/h.若不计队伍的长度,如图,折线A-B-C、A-D-E分别表示后队、联络员在行进过程中,离前队的路程y(km)与后队行进时间x(h)之间的部分函数图象.
(1)求线段AB对应的函数关系式;
(2)求点E的坐标,并说明它的实际意义;
(3)联络员从出发到他折返后第一次与后队相遇的过程中,当x为何值时,他离前队的路程与他离后队的路程相等?
【回归课本】我们曾学习过一个基本事实:两条直线被一组平行线所截,所得的对应线段成比例.
【初步体验】
(1)如图①,在△ABC中,点D、F在AB上,E、G在AC上,DE∥FG∥BC.若AD=2,AE=1,DF=6,则EG= , FB:GC = .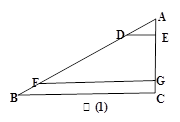
(2)如图②,在△ABC中,点D、F在AB上,E、G在AC上,且DE∥BC∥FG.以AD、DF、FB为边构造△ADM(即AM=BF,MD=DF);以AE、EG、GC为边构造△AEN(即AN=GC,NE=EG).
求证:∠M=∠N. 
【深入探究】
上述基本事实启发我们可以用“平行线分线段成比例”解决下列问题:
(3)如图③,已知△ABC和线段a,请用直尺与圆规作△A′B′C′,满足:①△A′B′C′∽△ABC;②△A′B′C′的周长等于线段a的长度.(保留作图痕迹,并写出作图步骤)











 中,自变量
中,自变量 的取值范围是 .
的取值范围是 . = .
= .

 ;
; .
. ;
; .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号