江苏省大丰市九年级下学期第一次调研检测数学试卷
如图,直线a∥b,直线DC与直线a相交于点C,与直线b相交于点D,已知∠1=25°,则∠2的度数为 ( )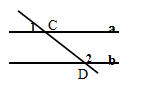
| A.135° | B.145° | C.155° | D.165° |
下列运算正确的是 ( )
A.2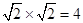 |
B.2a3•a4=2a12 | C.(2a4)3=8a7 | D.a8÷a2=a4 |
PM2.5是指大气中直径小于或等于2.5微米的颗粒物,2.5微米等于0.000 002 5米,把0.000 002 5用科学记数法表示为 ( )
| A.2.5×106 | B.0.25×10-5 | C.2.5×10-6 | D.25×10-7 |
某市3月下旬抽样六天的最高气温如下(单位℃):18,19,20,21,19,23,对这组数据下列说法错误的是 ( )
| A.平均数是20 | B.众数是19 |
| C.中位数是21 | D.都不正确 |
抛物线 上部分点的横坐标x纵坐标y的对应值如下表,则下列说法中错误的是 ( )
上部分点的横坐标x纵坐标y的对应值如下表,则下列说法中错误的是 ( )
| x |
… |
-4 |
-3 |
-2 |
-1 |
0 |
1 |
… |
| y |
… |
-37 |
-21 |
-9 |
-1 |
3 |
3 |
… |
A.当x>1时,y随x的增大而增大
B.抛物线的对称轴为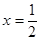 .
.
C.当x=2时,y=-1
D.方程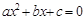 一个负数解
一个负数解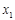 满足-1<
满足-1<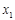 <0.
<0.
如图5,D是AB边上的中点,将 沿过D的直线折叠,使点A落在BC上F处,若∠B=50°,则∠BDF= __________度.
沿过D的直线折叠,使点A落在BC上F处,若∠B=50°,则∠BDF= __________度.
如图,两同心圆的圆心为O,大圆的弦AB切小圆于P,两圆的半径分别为6和3,则图中阴影部分的面积是 .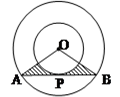
已知反比例函数y= 在第一象限的图象如图所示,点A在其图象上,点B为x轴正半轴上一点,连接AO、AB,且AO=AB,则S⊿AOB= .
在第一象限的图象如图所示,点A在其图象上,点B为x轴正半轴上一点,连接AO、AB,且AO=AB,则S⊿AOB= .
已知点P(x,y)位于第二象限,并且y≤x+4,x,y为整数,若以P为圆心,PO为半径画圆,则可以画出 个半径不同的圆来。
已知关于x的一元二次方程 +2x+2k-2=0有两个不相等的实数根.
+2x+2k-2=0有两个不相等的实数根.
(1)求k的取值范围;
(2)若k为正整数,求该方程的根.
如图1,某超市从一楼到二楼有一自动扶梯,图2是侧面示意图.已知自动扶梯AB的坡度为1:2.4,AB的长度是13米,MN是二楼楼顶,MN∥PQ,C是MN上处在自动扶梯顶端B点正上方的一点,BC⊥MN,在自动扶梯底端A处测得C点的仰角为42°,求二楼的层高BC约为多少米?( sin42°≈0.7,tan42°≈0.9)
去年以来,我国中东部地区持续出现雾霾天气.我市某记者为了了解“雾霾天气的主要成因”,随机调查了部分市民,并对调查结果进行整理,绘制了如下尚不完整的统计表:
请根据图表中提供的信息解答下列问题:
(1)填空:m= ,n= ,扇形统计图中E组所占的百分比为 ;
(2)若该市人口约有75万人,请你估计其中持D组“观点”的市民人数;
(3)若在这次接受调查的市民中,随机抽查一人,则此人持C组“观点”的概率是多少?
如图,在菱形ABCD中,AB=2,∠DAB=60°,点E是AD边的中点,点M是AB边上一动点(不与点A重合),延长ME交射线CD于点N,连接MD,AN.
(1)求证:四边形AMDN是平行四边形;
(2)填空:①当AM的值为 时,四边形AMDN是矩形;
②当AM的值为 时,四边形AMDN是菱形。
如图,已知AB是⊙O的直径,直线CD与⊙O相切于点C,AD⊥CD于点D.
(1)求证:AC平分∠DAB;
(2)若点E为 的中点,AD=
的中点,AD= ,AC=8,求AB和AE的长.
,AC=8,求AB和AE的长.
今年,6月12日为端午节.在端午节前夕,三位同学到某超市调研一种进价为2元的粽子的销售情况.请根据小丽提供的信息,解答小华和小明提出的问题.

(1)小华的问题解答:
(2)小明的问题解答:
将△ABC绕点A按逆时针方向旋转θ度,并使各边长变为原来的n倍,得△AB′C′,即如图①,我们将这种变换记为[θ,n].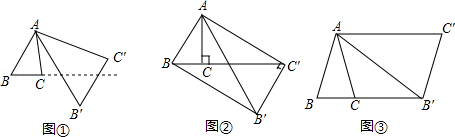
(1)如图①,对△ABC作变换[50°, ]得△AB′C′,则S△AB′C′:S△ABC= ;直线BC与直线B′C′所夹的锐角为 度;
]得△AB′C′,则S△AB′C′:S△ABC= ;直线BC与直线B′C′所夹的锐角为 度;
(2)如图②,△ABC中,∠BAC=30°,∠ACB=90°,对△ABC 作变换[θ,n]得△AB'C',使点B、C、C′在同一直线上,且四边形ABB'C'为矩形,求θ和n的值;
(3)如图③,△ABC中,AB=AC,∠BAC=36°,BC=l,对△ABC作变换[θ,n]得△AB′C′,使点B、C、B′在同一直线上,且四边形ABB'C'为平行四边形,求θ和n的值.


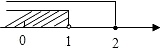
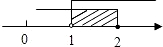
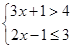 的解集在数轴上表示正确的是 ( )
的解集在数轴上表示正确的是 ( )

 与
与 是同类项,则m+n= .
是同类项,则m+n= . 的值为0,则x的值等于 .
的值为0,则x的值等于 . 在实数范围内有意义,则x的取值范围为 .
在实数范围内有意义,则x的取值范围为 .
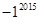 +
+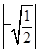 ﹣sin45°
﹣sin45° 
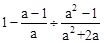 ,再选取一个合适的a值代入计算.
,再选取一个合适的a值代入计算. x+3与y轴交于点C,,与x轴交于点D.点P是x轴上方的抛物线上一动点,过点P作PF⊥x轴于点F,交直线CD于点E.设点P的横坐标为m。
x+3与y轴交于点C,,与x轴交于点D.点P是x轴上方的抛物线上一动点,过点P作PF⊥x轴于点F,交直线CD于点E.设点P的横坐标为m。
 粤公网安备 44130202000953号
粤公网安备 44130202000953号