福建省永春县八年级上学期期末质量检测数学试卷
记录一天气温的变化情况,选用比较合适的统计图是( )
| A.条形统计图 | B.扇形统计图 |
| C.折线统计图 | D.都不可以 |
如图,AB=AC,若要使△ABE≌△ACD,则添加的一个条件不能是( )
| A.∠B=∠C | B.BE=CD |
| C.BD=CE | D.∠ADC=∠AEB |
如图将4个长、宽分别均为 、
、 的长方形,摆成了一个大的正方形.利用面积的不同表示方法
的长方形,摆成了一个大的正方形.利用面积的不同表示方法
写出一个代数恒等式是( )
A. ; ; |
B. ; ; |
C. ; ; |
D. . . |
命题“如果两个角都是直角,那么这两个角相等”的逆命题是___________________________ .
如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形,若
正方形A、B、C、D的面积分别为2,5,1,2,则最大的正方形E的面积是__ __.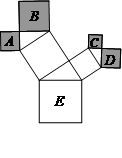
将两个斜边长相等的直角三角形纸片如图①放置,其中∠ACB=∠CED=90°,∠A=45°,∠D=30°.
①∠CBA= °;
②把△DCE绕点C顺时针旋转15°得到△D1CE1,如图②,连接D1B,则∠E1D1B= °.
如图,已知△ABC.
(1)作边AB的垂直平分线;
(2)作∠C的平分线.(要求:不写作法,保留作图痕迹)
为了解市民的学习爱好,有关部门统计了最近6个月到图书馆的读者的职业
分布情况,并做了下列两个不完整的统计图.
(1)本次共调查了多少人?
(2)将条形统计图补充完整;
(3)求“其它”所在扇形的圆心角的度数.
如图,在△ABC中,∠B=90°,AB=BC=4,点E在BC上,将△ABC沿AE折叠,
使点B落在AC边上的点F处.
(1)求BE的长;
(2)判断△CEF是什么特殊三角形.
在正方形ABCD中,AB=4.
(1)正方形ABCD的周长为 ;
(2)如图1,点E 、F分别在BC和AD上,点P 是线段EF上的动点,过点P作
EF的垂线L,若直线L与正方形CD、AB两边的交点分别为G、H.
①求证:EF=GH;
②已知,BE=2,AF=1,若线段PE的长度为 ,求
,求 的最小值;
的最小值;
③如图2,在②的条件下,已知AH= ,PE="2PF," 求图中阴影部分的面积.
,PE="2PF," 求图中阴影部分的面积.

(1)如图1,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°.E,F分别是BC,CD上的点.且∠EAF=60°,延长FD到点G,使DG=BE.连结AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得线段BE,EF,FD之间的数量关系为 .
(2)如图2,在四边形ABCD中,AB=AD,∠B+∠D=180°.E,F分别是BC,CD上的点,且∠EAF= ∠BAD,线段BE,EF,FD之间存在什么数量关系,为什么?
∠BAD,线段BE,EF,FD之间存在什么数量关系,为什么?
(3)如图3,点A在点O的北偏西30°处,点B在点O的南偏东70°处,且AO=BO,点A沿正东方向移动249米到达点E处,点B沿北偏东50°的方向移动334米到达点F处,从点O观测到E、F之间的夹角为70°,根据(2)的结论求E、F之间的距离.



 的结果是( )
的结果是( )



 分解因式,下列结果正确的是 ( )
分解因式,下列结果正确的是 ( )



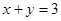 且
且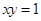 ,则代数式
,则代数式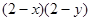 的值等于( ).
的值等于( ). = .
= . .
. (填入“>”或“<”号)
(填入“>”或“<”号) = .
= .



 ,其中
,其中 .
.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号