安徽省铜陵市四校九年级2月开学联考数学试卷
下列事件为必然事件的是( )
| A.小王参加本次数学考试,成绩是150分 |
| B.某射击运动员射靶一次,正中靶心 |
| C.打开电视机,中央一套节目正在播新闻 |
| D.口袋中装有两个红球和一个白球,从中摸出两个球,其中必有红球 |
如图,已知⊙O是△ABD的外接圆,AB是⊙O的直径,CD是⊙O的 弦, ∠ABD=58°,则∠BCD等于( )
| A.116° | B.64° | C.58° | D.32° |
把函数 =f(x)=
=f(x)= 的图象向左平移1个单位,再向上平移1个单位,所得图象对
的图象向左平移1个单位,再向上平移1个单位,所得图象对
应的函数的解析式是( )
| A.y=(x-3)2+3 | B.y=(x-3)2+1 |
| C.y=(x-1)2+3 | D.y=(x-1)2+1 |
已知函数y=(k-3)x2+2x+1的图象与x轴有交点,则k的取值范围是( )
| A.k<4 | B.k≤4 | C.k<4且k≠3 | D.k≤4且k≠3 |
如图,圆O1、圆O2的圆心O1、O2在直线l上,圆O1的半径为2 cm,圆O2的半径为3 cm,O1O2="8" cm。圆O1以1 cm/s的速度沿直线l向右运动,7s后停止运动,在此过程中,圆O1与圆O2没有出现的位置关系是( )
| A.外切 | B.相交 |
| C.内切 | D.内含 |
二次函数y=ax +bx+c(a≠0)的图象如图所示,下列结论:①c<0,②b>0,③4a+2b+c>0,④(a+c)
+bx+c(a≠0)的图象如图所示,下列结论:①c<0,②b>0,③4a+2b+c>0,④(a+c) <b
<b ,其中正确的有( )
,其中正确的有( )
| A.1个 | B.2个 | C.3个 | D.4个 |
如图,△ABC与△DEF均为等边三角形,O为BC、EF的中点,则AD:BE的值为( )
A. : 1 B.
: 1 B. : 1
: 1
C.5 : 3 D.不确定
如图,正方形ABCD的边长为3,点E,F分别在边AB,BC上,AE=BF=1,小球P从点E
出发沿直线向点F运动,每当碰到正方形的边时反弹,反弹时反射角等于入射角.当小球P第n(n为正整
数)次碰到点F时,小球P所经过的路程为( )
A. |
B. |
C. |
D. |
如果圆锥的底面周长是20π,侧面展开后所得的扇形的圆心角为120°,那么圆锥的侧面积是__________.(结果保留π)
如图,在等边△ABC中,D是边AC上的一点,连接BD,将△BCD绕点B逆时针旋转60°,得
到△BAE,连接ED,若BC=10,BD=9,则△AED的周长是______.
如图,等腰直角三角形ABC的顶点A,C在x轴上,∠ACB=90°, ,反比例
,反比例
函数 (
( )的图象分别与AB,BC交于点D,E.连接DE,当△BDE∽△BCA时,点E的坐标为______________.
)的图象分别与AB,BC交于点D,E.连接DE,当△BDE∽△BCA时,点E的坐标为______________.
如图,AB是⊙O的直径,AM、BN分别切⊙O于点A、B,CD交AM,BN于点D、C,DO平分∠ADC.
(1)求证:CD是⊙O的切线;
(2)若AD=4,BC=9,求⊙O的半径R.
图中的小方格都是边长为1的正方形,△ABC的顶点和O点都在正方形的顶点上.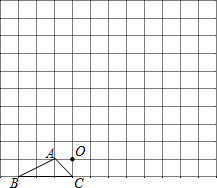
(1)以点O为位似中心,在方格图中将△ABC放大为原来的2倍,得到△A′B′C′;
(2)△A′B′C′绕点B′顺时针旋转90°,画出旋转后得到的△A″ C″,并求边A′B′在旋转过程中扫过的图形面积.
C″,并求边A′B′在旋转过程中扫过的图形面积.
2014年1月23日,安徽省省政府新闻办召开新闻发布会,通报了2013年全省经济运行情况。据省统计局新闻发言人赵金宝介绍,去年我省GDP突破19000亿元,连续第十年保持两位数增长,增速明显高于全国,位居中部第一。初步核算,全年全省生产总值19033.3亿元,按可比价格计算,比2011年增加3303.3亿元,连续10年保持两位数增长,增幅居全国第11、中部第1位。求自2011年起的年平均增长率。
如图,已知正比例函数y=2x和反比例函数的图象交于点A(m,-2).
(1)求反比例函数的解析式;
(2)观察图象,直接写出正比例函数值大于反比例函数值时自变量x的取值范围;
(3)若双曲线上点C(2,n)沿OA方向平移 个单位长度得到点B,判断四边形OABC的形状并证明你的结论.
个单位长度得到点B,判断四边形OABC的形状并证明你的结论.
为了贯彻“减负增效”精神,掌握九年级600名学生每天的自主学习情况,二中学生会随机抽查了九年级的部分学生,并调查他们每天自主学习的时间,根据调查结果,制作了两幅不完整的统计图(图1,图2),请根据统计图中的信息回答下列问题:
(1)本次调查的学生人数是 人.
(2)图2中α是 度,并将图1条形统计图补充完整.
(3)请估算该校九年级学生自主学习的时间不少于1.5小时有 人.
(4)老师想从学习效果较好的4位同学(分别记为A、B、C、D,其中A为小亮)随机选择两位进行学习经验交流,用列表法或树状图的方法求出选中小亮A的概率.
铜陵学院毕业生小张响应国家“自主创业”的号召,投资开办了一个装饰品商店,该店采购进一种今年新上市的饰品进行了30天的试销售,购进价格为20元/件。销售结束后,得知日销售量P(件)与销售时间x(天)之间有如下关系:P=-2x+80(1≤x≤30,且x为整数);又知前20天的销售价格Q1(元/件)与销售时间x(天)之间有如下关系: (1≤x≤20,且x为整数),后10天的销售价格Q2(元/件)与销售时间x(天)之间有如下关系:Q2=45(21≤x≤30,且x为整数)。
(1≤x≤20,且x为整数),后10天的销售价格Q2(元/件)与销售时间x(天)之间有如下关系:Q2=45(21≤x≤30,且x为整数)。
(1)第25天该商店的日销售利润为多少元?
(2)试写出该商店日销售利润y(元)关于销售时间x(天)之间的函数关系式;
(2)请问在这30天的试销售中,哪一天的日销售利润最大?并求出这个最大利润。
如图,将边长为4的等边三角形AOB放置于平面直角坐标系xOy中,F是AB边上的动点(不与点A,B重合),过点F的反比例函数 (
( ,
, )与OA边交于点E,过点F作FC⊥x轴于点C,连接EF,OF.
)与OA边交于点E,过点F作FC⊥x轴于点C,连接EF,OF.
(1)若 ,求反比例函数的解析式.
,求反比例函数的解析式.
(2)在(1)的条件下,试判断以点E为圆心,EA长为半径的圆与 轴的位置关系,并说明理由.
轴的位置关系,并说明理由.
(3)AB边上是否存在点F,使得EF⊥AE?若存在,请求出BF:FA的值;若不存在,请说明理由.

 的一个根,则这个方程的另一个根是( )
的一个根,则这个方程的另一个根是( )


 与x轴的两个交点分别为A(-3,0),B
与x轴的两个交点分别为A(-3,0),B 轴上是否存在点D,使得△ACD是以AC为斜边的直角三角形?若存在,求出点D的坐标;若不存在,说明理由.
轴上是否存在点D,使得△ACD是以AC为斜边的直角三角形?若存在,求出点D的坐标;若不存在,说明理由.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号