浙江省温州市名校七年级上学期1月联考数学试卷
已知 在数轴上对应的点在0和-1之间,则
在数轴上对应的点在0和-1之间,则 对应的各点中,离原点最远的是( ).
对应的各点中,离原点最远的是( ).
A. |
B. |
C. |
D. |
若方程组 无解,则( ).
无解,则( ).
A. 可取任意常数 可取任意常数 |
B. 可取任意常数 可取任意常数 |
C. 可取任意常数, 可取任意常数, |
D. |
若 表示一个整数,则整数x可取的值共有( ).
表示一个整数,则整数x可取的值共有( ).
| A.8个 | B.4个 | C.3个 | D.2个 |
如图所示的数阵叫“莱布尼兹调和三角形”,它是由整数的倒数组成的,第n行有n个数,且两端的数都为 ,每个数是它下一行左右相邻两数的和,则第8行第3个数(从左往右数)为( ).
,每个数是它下一行左右相邻两数的和,则第8行第3个数(从左往右数)为( ).
A. |
B. |
C. |
D. |
如图,已知正方形ABCD和CEFG的边长分别为m,n,那么△AEG的面积的值( ).
| A.只与m的大小有关 | B.只与n的大小有关 |
| C.与m、n的大小都有关 | D.与m、n的大小都无关 |
把下列数:7的平方根、7的立方根、7的相反数、7的倒数从小到大的顺序用“<”连接排列为 .
如图所示,数轴上点A表示的数是-1,O是原点,以AO为边作正方形AOBC,以A为圆心、AB长为半径画弧交数轴于P1、P2 两点,则点P1表示的数是 .(结果精确到 ,参考数据:
,参考数据: ).
).
让我们轻松一下,做一个数字游戏.第一步:取一个自然数 ,计算
,计算 得
得 ;第二步:算出
;第二步:算出 的各位数字之和得
的各位数字之和得 ,计算
,计算 得
得 ;第三步:算出
;第三步:算出 的各位数字之和得
的各位数字之和得 ,计算
,计算 得
得 ;……依次类推:则
;……依次类推:则 =
=
如图,线段AB表示一条对折的绳子,现从P点处将绳子剪断,剪断后的各段绳子中最长的一段为30cm,若 ,则原来绳长_________cm.
,则原来绳长_________cm.
(本题8分)男女运动员各一名在环形跑道上练习长跑,男运动员比女运动员速度快,他们从同一起点沿相反方向同时出发,每隔25秒相遇一次.现在他们从同一起跑点沿相同方向同时出发,经过25分钟男运动员追上女运动员,并且比女运动员多跑20圈.
求 (1) 男运动员的速度是女运动员的多少倍?
(2) 男运动员追上女运动员时,女运动员跑了多少圈?
(本题12分)如图1,CE平分∠ACD,AE平分∠BAC,∠EAC+∠ACE=90°
(1)请判断AB与CD的位置关系并说明理由;
(2)如图2,当∠E=90°保持不变,移动直角顶点E,使∠MCE=∠ECD,当直角顶点E点移动时,问∠BAE与∠MCD否存在确定的数量关系?并说明理由;;
(3)如图3,P为线段AC上一定点,点Q为直线CD上一动点,①当点Q在射线CD上运动时(点C除外)∠CPQ+∠CQP与∠BAC有何数量关系?猜想结论并说明理由.②当点Q在射线CD的反向延长线上运动时(点C除外)∠CPQ+∠CQP与∠BAC有何数量关系?直接写出猜想结论,不需说明理由.
 ,则
,则 是( ).
是( ). ,则
,则 等于( ).
等于( ). 满足
满足 ,那么
,那么 的值为( ).
的值为( ).



 是 次多项式,它二次项系数之和是 .
是 次多项式,它二次项系数之和是 .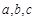 在数轴上的位置如图,则化简
在数轴上的位置如图,则化简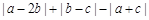 的结果为___.
的结果为___.

 ,求
,求 的值.
的值. 中恰有三个数相等,求
中恰有三个数相等,求 的值.
的值. 的值.
的值. 粤公网安备 44130202000953号
粤公网安备 44130202000953号