山东省滨州市八年级上学期期末考试数学试卷
已知图中的两个三角形全等,则∠α度数是( )
| A.50° | B.58° | C.60° | D.72° |
若等腰三角形中有一个角等于 ,则这个等腰三角形的顶角的度数为( )
,则这个等腰三角形的顶角的度数为( )
A. |
B. |
C. 或 或 |
D. 或 或 |
使分式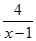 有意义,则x的取值范围是( )
有意义,则x的取值范围是( )
| A.x ≠ 1 | B.x>1 | C.x<1 | D.x ≠-1 |
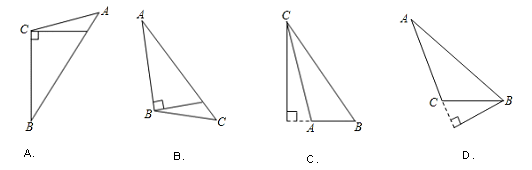
下列判定两个直角三角形全等的方法,错误的是 ( )
| A.两条直角边对应相等 | B.斜边和一锐角对应相等 |
| C.斜边和一直角边对应相等 | D.两锐角对应相等 |
如图,已知△ABC,O是△ABC内的一点,连接OB、OC,将∠ABO、∠ACO分别记为∠1、∠2,则∠1、∠2、∠A、∠O四个角之间的数量关系是( )
A.∠1+∠0=∠A+∠2 B.∠1+∠2+∠A+∠O=180°
C.∠1+∠2+∠A+∠O=360° D.∠1+∠2+∠A=∠O
已知:如图,AB=AC,∠A=36°,AB的垂直平分线交AC于D,则下列结论:
(1)∠C=72°,
(2)BD是∠ABC的平分线,
(3)△ABD是等腰三角形,
(4)△BCD∽△ABC,
其中正确的有( )
| A.4个 | B.3个 | C.2个 | D.1个 |
如图,已知△ABC中,AB=AC,点D、E在BC上,要使△ABD≌△ACE,则只需添加一个适当的条件是________________.(只填一个即可)
我们已经学过用面积来说明公式.如 就可以用下图甲中的面积来说明.
就可以用下图甲中的面积来说明.
请写出图乙的面积所说明的公式:x2+(p+q)x+pq = .
如图所示,在△ABC中,AE、BF是角平分线,它们相交于点O,AD是高,∠BAC=54°,∠C=66°,求∠DAC、∠BOA的度数.
从2014年春季开始,我县农村实行垃圾分类集中处理,对农村环境进行综合整治,靓化了我们的家园。现在某村要清理一个卫生死角内的垃圾,若用甲、乙两车运送,两车各运15趟可完成,已知甲、乙两车单独运完此堆垃圾,乙车所运趟数是甲车的3倍,求甲、乙两车单独运完此堆垃圾各需运多少趟?
如图,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上一点,点E在BC边上,且BE=BD,连结AE、DE、DC.
①求证:△ABE≌△CBD;
②若∠CAE=33°,求∠BDC的度数.
常用的分解因式的方法有提取公因式法、公式法及到了高中还要学习的十字相乘法,但有更多的多项式只用上述方法就无法分解,如 ,我们细心观察这个式子就会发现,前两项符合平方差公式,后两项可提取公因式,前后两部分分别分解因式后会产生公因式,然后提取公因式就可以完成整个式子的分解因式了。过程为:
,我们细心观察这个式子就会发现,前两项符合平方差公式,后两项可提取公因式,前后两部分分别分解因式后会产生公因式,然后提取公因式就可以完成整个式子的分解因式了。过程为: =
= =
=
这种分解因式的方法叫分组分解法。利用这种方法解决下列问题:
(1)分解因式 ;
;
(2) 三边a,b,c满足
三边a,b,c满足 ,判断
,判断 的形状。
的形状。
如图,在等边△ABC中,∠ABC与∠ACB的平分线相交于点O,且OD∥AB,OE∥AC.
(1)试判定△ODE的形状。并说明你的理由.
(2)线段BD、DE、EC三者有什么关系?写出你的判断过程.









 ,则分式
,则分式  的值等于( )
的值等于( )

 有增根,则k= _________ .
有增根,则k= _________ .

 ,其中x=2.
,其中x=2. 与
与 的值相等?
的值相等?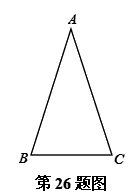
 粤公网安备 44130202000953号
粤公网安备 44130202000953号