小学奥数数论专题——数位与进制
(美国小学数学奥林匹克)把一个两位数的十位与个位上的数字加以交换,得到一个新的两位数.如果原来的两位数和交换后的新的两位数的差是45,试求这样的两位数中最大的是多少?
将一个四位数的数字顺序颠倒过来,得到一个新的四位数(这个数也叫原数的反序数),新数比原数大8802.求原来的四位数.
如果一个自然数的各个数码之积加上各个数码之和,正好等于这个自然数,我们就称这个自然数为“巧数”。例如,99就是一个巧数,因为9×9+(9+9)=99。可以证明,所有的巧数都是两位数。请你写出所有的巧数。
从1~9九个数字中取出三个,用这三个数可组成六个不同的三位数。若这六个三位数之和是3330,则这六个三位数中最小的可能是几?最大的可能是几?
a,b,c分别是 中不同的数码,用a,b,c共可组成六个三位数,如果其中五个三位数
中不同的数码,用a,b,c共可组成六个三位数,如果其中五个三位数
之和是2234,那么另一个三位数是几?
在两位自然数的十位与个位中间插入0~9中的一个数码,这个两位数就变成了三位数,有些两位数中间插入某个数码后变成的三位数,恰好是原来两位数的9倍。求出所有这样的三位数。
一辆汽车进入高速公路时,入口处里程碑上是一个两位数,汽车匀速行使,一小时后看到里程碑上的数是原来两位数字交换后的数。又经一小时后看到里程碑上的数是入口处两个数字中间多一个0的三位数,请问:再行多少小时,可看到里程碑上的数是前面这个三位数首末两个数字交换所得的三位数。
将四位数的数字顺序重新排列后,可以得到一些新的四位数.现有一个四位数码互不相同,且没有0的四位数 ,它比新数中最大的小3834,比新数中最小的大4338.求这个四位数.
,它比新数中最大的小3834,比新数中最小的大4338.求这个四位数.
有一个两位数,如果把数码3加写在它的前面,则可得到一个三位数,如果把数码3加写在它的后面,则可得到一个三位数,如果在它前后各加写一个数码3,则可得到一个四位数.将这两个三位数和一个四位数相加等于 .求原来的两位数.
.求原来的两位数.
将4个不同的数字排在一起,可以组成24个不同的四位数( ).将这24个四位数按从小到大的顺序排列的话,第二个是5的倍数;按从大到小排列的话,第二个是不能被4整除的偶数;按从小到大排列的第五个与第二十个的差在3000~4000之间.求这24个四位数中最大的那个.
).将这24个四位数按从小到大的顺序排列的话,第二个是5的倍数;按从大到小排列的话,第二个是不能被4整除的偶数;按从小到大排列的第五个与第二十个的差在3000~4000之间.求这24个四位数中最大的那个.
 和它的反序数
和它的反序数 的差被99除,商等于______与______的差;
的差被99除,商等于______与______的差; 与
与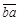 的差被9除,商等于______与______的差;
的差被9除,商等于______与______的差; 与
与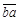 的和被11除,商等于______与______的和。
的和被11除,商等于______与______的和。 .
. ,这里A表示一个看不清的数码,求这个数和A。
,这里A表示一个看不清的数码,求这个数和A。 ,它与3的乘积形如
,它与3的乘积形如 ,则七位数
,则七位数 应是多少?
应是多少?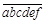 ,如果满足
,如果满足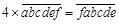 ,则称
,则称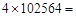
 ,则102564就是“迎春数”).请你求出所有“迎春数”的总和.
,则102564就是“迎春数”).请你求出所有“迎春数”的总和. 满足
满足 ,请写出这样的六位数.
,请写出这样的六位数.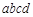 为
为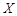 ,由它的四个数字a,b,c,d组成的最小的四位数记为
,由它的四个数字a,b,c,d组成的最小的四位数记为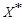 ,如果
,如果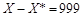 ,那么这样的四位数
,那么这样的四位数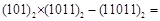 ________;
________;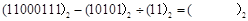 ;
;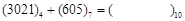 ;
;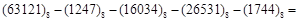 ________;
________;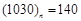 ,则
,则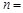 ________.
________. ;
;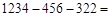 ________;
________;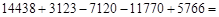 ________.
________. ?
? ?
? 是几进制数的乘法?
是几进制数的乘法?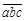 ,化为9进制为
,化为9进制为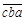 ,求这个三位数在十进制中为多少?
,求这个三位数在十进制中为多少?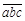 ,化为9进制为
,化为9进制为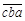 ,求这个三位数在十进制中为多少?
,求这个三位数在十进制中为多少? -1)除以992的余数是多少?
-1)除以992的余数是多少? 除以26的余数.
除以26的余数. 除以7的余数.
除以7的余数. 的八进制表示为
的八进制表示为 ,那么在十进制下,
,那么在十进制下, 粤公网安备 44130202000953号
粤公网安备 44130202000953号