如图所示,如量为m=0.8kg的砝码悬挂在轻绳PA和PB的结点上并处于静止状态.PA与竖直方向的夹角37°,PB沿水平方向.质量为M=10kg的木块与PB相连,静止于倾角为37°的斜面上,sin53°=0.80,cos53°=0.60,取重力加速度g=10m/s2。求: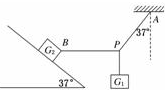
(1)轻绳PB拉力的大小;
(2)木块所受斜面的摩擦力和弹力大小.
相关知识点
如图所示,如量为m=0.8kg的砝码悬挂在轻绳PA和PB的结点上并处于静止状态.PA与竖直方向的夹角37°,PB沿水平方向.质量为M=10kg的木块与PB相连,静止于倾角为37°的斜面上,sin53°=0.80,cos53°=0.60,取重力加速度g=10m/s2。求:
(1)轻绳PB拉力的大小;
(2)木块所受斜面的摩擦力和弹力大小.