如图所示,两平行光滑导轨相距为L=20cm,金属棒MN的质量为m=10g,电阻R=8Ω,匀强磁场的磁感应强度B=0.8T,方向竖直向下,电源电动势E=10V,内阻r=1Ω,当开关S闭合时,MN恰好平衡.
求变阻器R1的取值为多少?设θ=45°,g取10m/s2.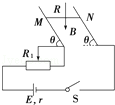
如图所示,两平行光滑导轨相距为L=20cm,金属棒MN的质量为m=10g,电阻R=8Ω,匀强磁场的磁感应强度B=0.8T,方向竖直向下,电源电动势E=10V,内阻r=1Ω,当开关S闭合时,MN恰好平衡.
求变阻器R1的取值为多少?设θ=45°,g取10m/s2.