质绳跨过光滑轻质滑轮与物体B相连接，B的质量M=1kg，绳绷直时B离地面有一定高度．在t=0时刻，无初速度释放B，由固定在A上的速度传感器得到的数据绘出的A沿斜面向上运动的v﹣t图象如图乙所示，若B落地后不反弹，g取10m/s2，sin37°=0.6，cos37°=0.8，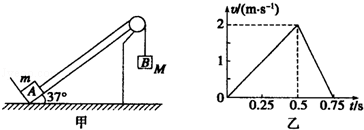
（1）B下落的加速度大小为多少？
（2）A沿斜面向上运动的过程中，绳的拉力对A做的功为多少？
（3）A的质量M=0.5kg，A与斜面间的动摩擦因数μ为多少？
（4）0～0.75s内摩擦力对A做的功是多少？
跳伞运动员做低空跳伞表演，他离开飞机后先做自由落体运动，当距离地面 104m时打开降落伞，伞张开后运动员就以12 m/s2的加速度做匀减速运动，到达地面时速度为2 m/s，问：
(1) 刚打开降落伞时运动员的速度为多少？
(2) 运动员离开飞机时距地面的高度为多少?
(3)离开飞机后，经过多少时间才能到达地面?(g="10" m/s)
一辆公共汽车从车站开出，以8 m/s的速度沿平直公路匀速行驶,经过2s后,一辆摩托车从同一车站由静止开始做匀加速直线运动追赶公共汽车，加速度为6 m/s2.问：
（1）摩托车出发后,经多长时间追上汽车?
（2）摩托车追上汽车之前，两车相距最远的距离是多少？
如图所示，光滑水平面上有一质量M=4.0kg的带有圆弧轨道的平板车，车的上表面是一段长L=1.0m的粗糙水平轨道，水平轨道左侧连一半径R="0.25m" 的
光滑圆弧轨道，圆弧轨道与水平轨道在O′点相切。车右端固定一个尺寸可以忽略、处于锁定状态的压缩弹簧，一质量m=1.0kg的小物块紧靠弹簧放置，小物块与水平轨道间的动摩擦因数μ=0.5。整个装置处于静止状态，现将弹簧解除锁定，小物块被弹出，恰能到达圆弧轨道的最高点A。取g=10m/2，求：
(1) 小物块到达A点时，平板车的速度大小
(2) 解除锁定前弹簧的弹性势能；
(3) 小物块第二次经过O′点时的速度大小；
(4) 小物块与车最终相对静止时，它距O′点的距离。
粤公网安备 44130202000953号