如图所示,物体从光滑斜面的顶端A点由静止开始下滑做匀加速直线运动,经过B点后进入粗糙的水平面(设经过B点前后速度大小不变)做匀减速直线运动,最后停在C点,每隔0.2s通过速度传感器测量物体的速度,下表给出了部分测量数据(g取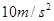 )
)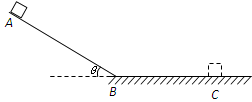

求:(1)在水平面上匀减速运动的加速度大小
(2)从开始运动到停止所用的总时间
(3)斜面的长度L
如图所示,物体从光滑斜面的顶端A点由静止开始下滑做匀加速直线运动,经过B点后进入粗糙的水平面(设经过B点前后速度大小不变)做匀减速直线运动,最后停在C点,每隔0.2s通过速度传感器测量物体的速度,下表给出了部分测量数据(g取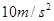 )
)

求:(1)在水平面上匀减速运动的加速度大小
(2)从开始运动到停止所用的总时间
(3)斜面的长度L