如图所示，一质量m="l" 0kg的小物块静止在粗糙水平台阶上，离台阶边缘O点的距离s=5m，它与水平台阶表面的动摩擦因数μ="0" 25。在台阶右侧固定一个以O为圆心的 
圆弧挡板，圆弧半径R=5
m，以O点为原点建立平面直角坐标系xOy。现用F=5N的水平恒力拉动小物块（已知重力加速度g=l0m/s2）。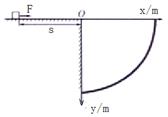
（1）为使小物块不落在挡板上，求拉力F作用的最长距离
（2）（2）若小物块在水平台阶上运动时，拉力F一直作用在小物块上，当小物块过O点时撤去拉力F，求小物块击中挡板上的位置的坐标。
如图所示，质量为M的斜劈静止于粗糙水平地面上，质量为m的滑块在斜面上匀速下滑，已知斜面足够长，倾角为θ，某时刻对滑块m施加一个与斜面夹角为φ的力F，滑块开始加速下滑，重力加速度取g，求：
（1）滑块m的加速度a；
（2）M受到的地面的摩擦力f；
（3）讨论将外力F逆时针转过90º的过程中，若滑块m一直下滑，地面对M的摩擦力f的变化情况。
如图所示。竖直放置的间距为L的两平行光滑导轨，上端连接一个阻值为R的电阻，在导轨的MN位置以下有垂直纸面向里的磁场，在MN处的磁感应强度为B0，在MN下方的磁场沿Y轴方向每单位长度磁感应强度减少kT。现有一质量为m，电阻也是R的金属棒，从距离MN为h的上方紧贴导轨自由下落，然后进入磁场区域继续下落h的过程中，能使得电阻R上的电功率保持不变（不计一切摩擦）求：
（1）电阻R上的电功率；
（2）从MN位置再下降h时，金属棒的速度v；
（3）从MN位置再下降h所用的时间t。
两物块A、B用轻弹簧相连，质量均为2 kg，初始时弹簧处于原长，A、B两物块都以v＝6 m／s的速度在光滑的水平地面上运动，质量4 kg的物块C静止在前方，如图所示。B与C碰撞后二者会粘在一起运动。求在以后的运动中：
（1）当弹簧的弹性势能最大时，物块A的速度为多大?
（2）系统中弹性势能的最大值是多少?
(18分)如图所示，竖直平面内有无限长、不计电阻的两组平行光滑金属导轨，宽度均为L=0.5m，上方连接一个阻值R=1Ω的定值电阻，虚线下方的区域内存在磁感应强度B=2T的匀强磁场．完全相同的两根金属杆1和2靠在导轨上，金属杆与导轨等宽且与导轨接触良好，电阻均为r=0.5Ω．将金属杆1固定在磁场的上边缘（仍在此磁场内），金属杆2从磁场边界上方h0=0.8m处由静止释放，进入磁场后恰作匀速运动．(g取10m/s2)求：
（1）金属杆的质量m为多大？
（2）若金属杆2从磁场边界上方h1=0.2m处由静止释放，进入磁场经过一段时间后开始匀速运动．在此过程中整个回路产生了1.4J的电热，则此过程中流过电阻R的电量q为多少？
（3）金属杆2仍然从离开磁场边界h1=0.2m处由静止释放，在金属杆2进入磁场的同时由静止释放金属杆1，两金属杆运动了一段时间后均达到稳定状态，试求两根金属杆各自的最大速度．（已知两个电动势分别为E1、E2不同的电源串联时，电路中总的电动势E=E1+E2．）
（单位：m），小物块质量m =" 0.4" kg，坡面高度h =" 0.4" m，小物块从坡面上滑下时克服摩擦力做功1 J，小物块与平台表面间的动摩擦因数μ = 0.1，g =" 10" m/s2．求
粤公网安备 44130202000953号