如图所示,在水平地面上固定一个倾角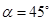 、高H=4m的斜面,在斜面上方固定放置一段由内壁光滑的圆管构成的轨道ABCD,圆周部分的半径
、高H=4m的斜面,在斜面上方固定放置一段由内壁光滑的圆管构成的轨道ABCD,圆周部分的半径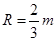 ,AB与圆周相切于B点,长度为
,AB与圆周相切于B点,长度为 ,与水平方向夹角
,与水平方向夹角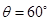 ,轨道末端竖直,已知圆周轨道最低点C.轨道末端D与斜面顶端处于同一高度。现将一质量为0.1kg,直径可以忽略的小球从管口A处由静止释放,
,轨道末端竖直,已知圆周轨道最低点C.轨道末端D与斜面顶端处于同一高度。现将一质量为0.1kg,直径可以忽略的小球从管口A处由静止释放,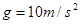
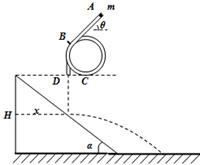
(1)求小球在C点时对轨道的压力
(2)若小球与斜面碰撞(不计能量损失)后做平抛运动落到水平地面上,则碰撞点距斜面左端的水平距离x多大时小球平抛运动的水平位移最大?最大位移是多少?
如图所示,在水平地面上固定一个倾角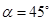 、高H=4m的斜面,在斜面上方固定放置一段由内壁光滑的圆管构成的轨道ABCD,圆周部分的半径
、高H=4m的斜面,在斜面上方固定放置一段由内壁光滑的圆管构成的轨道ABCD,圆周部分的半径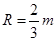 ,AB与圆周相切于B点,长度为
,AB与圆周相切于B点,长度为 ,与水平方向夹角
,与水平方向夹角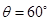 ,轨道末端竖直,已知圆周轨道最低点C.轨道末端D与斜面顶端处于同一高度。现将一质量为0.1kg,直径可以忽略的小球从管口A处由静止释放,
,轨道末端竖直,已知圆周轨道最低点C.轨道末端D与斜面顶端处于同一高度。现将一质量为0.1kg,直径可以忽略的小球从管口A处由静止释放,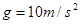

(1)求小球在C点时对轨道的压力
(2)若小球与斜面碰撞(不计能量损失)后做平抛运动落到水平地面上,则碰撞点距斜面左端的水平距离x多大时小球平抛运动的水平位移最大?最大位移是多少?