如图所示，轻绳OA、OB与OC悬挂一质量为m的物体，OA与水平方向夹角为60°，OB位于水平方向．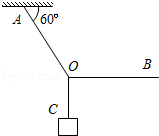
（1）求OB绳上的拉力的大小T1；
（2）若保持O点位置不变，将OB由水平位置绕O点逆时针缓慢旋转30°，求此位置处OB上拉力的大小T2；
（3）若保持O点位置不变，将OB由水平位置绕O点逆时针缓慢转动90°，求此过程中OB上拉力的最大值Tmax和最小值Tmin．
如图所示，固定于同一条竖直线上的A、B是两个带等量异种电荷的点电荷，电荷量分别为＋Q和－Q，A、B相距为2d。MN是竖直放置的光滑绝缘细杆，另有一个穿过细杆的带电小球p，其质量为m、电荷量为＋q(可视为点电荷，不影响电场的分布)，现将小球p从与点电荷A等高的C处由静止开始释放，小球p向下运动到距C点距离为d的O点时，速度为v，已知MN与AB之间的距离为d，静电力常量为k，重力加速度为g。求：
（1）C、O间的电势差UCO；
（2）小球p在O点时的加速度；
（3）小球p经过与点电荷B等高的D点时的速度。
如图(甲)所示，质量m="2" kg的物体在水平面上向右做直线运动。过P点时给物体作用一个水平向左的恒力F并开始计时，选取水平向右为速度的正方向，通过速度传感器测出物体的瞬时速度，所得v
t图像如图(乙)所示。取重力加速度为g="10" m/s2。求：
（1）物体在0～4 s内和4～10 s内的加速度a1、a2的大小；
（2）力F的大小和物体与水平面间的动摩擦因数μ；
（3）10 s末物体离P点的距离。
在如图甲所示的平面坐标系内，有三个不同的静电场：第一象限内有电荷量为Q的点电荷在O点产生的电场E1，第二象限内有水平向右的匀强电场E2，第四象限内有方向水平、大小按图乙变化的电场E3，E3以水平向右为正方向，变化周期
。一质量为m，电荷量为+q的离子从（-x0，x0）点由静止释放，进入第一象限后恰能绕O点做圆周运动。以离子经过x轴时为计时起点，已知静电力常量为k，不计离子重力。求：
（1）离子刚进入第四象限时的速度；
（2）E2的大小；
（3）当t=
时，离子的速度；
（4）当t=nT时，离子的坐标。
起重机从静止开始起吊一质量为4000kg重物，开始，起重机拉力恒定，重物以0.2 m/s2的加速度匀加速上升，9.8s后，起重机达到额定功率P，起重机再保持额定功率不变，又经5s，重物达到最大速度2m/s，此后再保持拉力恒定，使重物以0.5m/s2的加速度做匀减速运动至停下。取g=9.8m/s2.
（1）求额定功率P的大小；
（2）求重物上升的最大高度；
（3）在图示坐标纸上画出整个过程起重机拉力F与时间t的关系图象（不要求写计算过程）。
粤公网安备 44130202000953号