如图1所示的平行板电容器，板间距为d，两板所加电压随时间的变化如图2所示，t=0时刻，质量为m、带电量为q的粒子以平行于极板的速度v0射入电容器，t=3T时斜射出电容器，不计带电粒子的重力，求：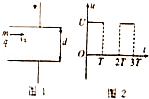
（1）平行板电容器板长L；
（2）粒子射出电容器时速度方向偏转的角度的正切值；
（3）粒子射出电容器时垂直极板方向偏转的距离y．
如图，有一水平传送带以2m／s的速度匀速运动，现将一物体轻轻放在传送带的左端上，已知物体与传送带间的动摩擦因数为0.5，传送带左、右端间的距离为10m，求传送带将该物体传送到传送带的右端所需时间。(g取10 m/s2 ) 
如图所示，匀强电场区域和匀强磁场区域是紧邻的且宽度相等均为d，电场方向在纸平面内，而磁场方向垂直纸面向里．一带正电粒子从O点以速度v0沿垂直电场方向进入电场．在电场力的作用下发生偏转，从A点离开电场进入磁场，离开电场时带电粒子在电场方向的偏移量为d，当粒子从C点穿出磁场时速度方向与进入电场O点时的速度方向一致，不计带电粒子的重力，求：
粒子从C点穿出磁场时的速度v.
电场强度和磁感应强度的比值.
如图所示，在平面直角坐标xOy内，第I象限有沿一y方向的匀强电场，第IV象限有垂直于纸面向外的匀强磁场。现有一质量为m、带电量为+q的粒子（重力不计）以初速度v0沿-x方向从坐标为（3l,l）的P点开始运动，接着进人磁场后由坐标原点O射出，射出时速度方向与y轴方向夹角为45°，求
粒子从O点射出时的速度v;
电场强度E的大小；
粒子从P点运动到O点所用的时间。
滑板运动是青少年喜爱的一项活动。如图所示，滑板运动员以某一初速度从A点水平离开h="O." 8 m髙的平台，运动员（连同滑板）恰好能无碰撞的从B点沿圆弧切线进人竖直光滑圆弧轨道，然后经C点沿固定斜面向上运动至最高点D。圆弧轨道的半径为1 m ,B、C为圆弧的两端点，其连线水平，圆弧对应圆心角
，斜面与圆弧相切于C点。已知滑板与斜面间的动摩擦因数为
，不计空气阻力，运动员（连同滑板）质量为50 kg,可视为质点。试求：
运动员（连同滑板)离开平台时的初速度v0；
运动员（连同滑板)通过圆弧轨道最底点对轨道的压力；
运动员（连同滑板）在斜面上滑行的最大距离。
粤公网安备 44130202000953号