质量为4m的小物块A静止在离地面高h的水平桌面的边缘,质量为m的小物块B沿桌面向A运动以速度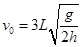 与之发生正碰(碰撞时间极短)。碰后A离开桌面,其落地点离出发点的水平距离为L,碰后B反向运动。已知B与桌面间的动摩擦因数为μ,重力加速度为g,求:
与之发生正碰(碰撞时间极短)。碰后A离开桌面,其落地点离出发点的水平距离为L,碰后B反向运动。已知B与桌面间的动摩擦因数为μ,重力加速度为g,求:
(1)B后退的距离为多少?
(2)整个运动过程中,物块B克服摩擦力做的功与因碰撞损失的机械能之比为多少
质量为4m的小物块A静止在离地面高h的水平桌面的边缘,质量为m的小物块B沿桌面向A运动以速度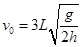 与之发生正碰(碰撞时间极短)。碰后A离开桌面,其落地点离出发点的水平距离为L,碰后B反向运动。已知B与桌面间的动摩擦因数为μ,重力加速度为g,求:
与之发生正碰(碰撞时间极短)。碰后A离开桌面,其落地点离出发点的水平距离为L,碰后B反向运动。已知B与桌面间的动摩擦因数为μ,重力加速度为g,求:
(1)B后退的距离为多少?
(2)整个运动过程中,物块B克服摩擦力做的功与因碰撞损失的机械能之比为多少