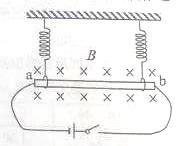
如图，一长为10cm的金属棒用两个完全相同的弹簧水平地悬挂在匀强磁场中；磁场的磁感应强度大小为0.1T，方向垂直于纸面向里；弹簧上端固定，下端与金属棒绝缘，金属棒通过开关与一电动势为12V的电池相连，电路总电阻为2。已知开关断开时两弹簧的伸长量均为0.5cm；闭合开关，系统重新平衡后，两弹簧的伸长量与开关断开时相比均改变了0.3cm，重力加速度大小取。判断开关闭合后金属棒所受安培力的方向,并求出金属棒的质量。
算盘是我国古老的计算工具，中心带孔的相同算珠可在算盘的固定导杆上滑动，使用前算珠需要归零，如图所示，水平放置的算盘中有甲、乙两颗算珠未在归零位置，甲靠边框b，甲、乙相隔 ，乙与边框a相隔 ，算珠与导杆间的动摩擦因数 。现用手指将甲以 的初速度拨出，甲、乙碰撞后甲的速度大小为 ，方向不变，碰撞时间极短且不计，重力加速度g取 。
（1）通过计算，判断乙算珠能否滑动到边框a；
（2）求甲算珠从拨出到停下所需的时间。
如图，间距为l的光滑平行金属导轨，水平放置在方向竖直向下的匀强磁场中，磁场的磁感应强度大小为B，导轨左端接有阻值为R的定值电阻，一质量为m的金属杆放在导轨上。金属杆在水平外力作用下以速度 向右做匀速直线运动，此时金属杆内自由电子沿杆定向移动的速率为 。设金属杆内做定向移动的自由电子总量保持不变，金属杆始终与导轨垂直且接触良好，除了电阻R以外不计其它电阻。
（1）求金属杆中的电流和水平外力的功率；
（2）某时刻撤去外力，经过一段时间，自由电子沿金属杆定向移动的速率变为 ，求：
（i）这段时间内电阻R上产生的焦耳热；
（ii）这段时间内一直在金属杆内的自由电子沿杆定向移动的距离。
如图，一长木板在光滑的水平面上以速度 向右做匀速直线运动，将一小滑块无初速地轻放在木板最右端。已知滑块和木板的质量分别为m和2m，它们之间的动摩擦因数为μ，重力加速度为g。
（1）滑块相对木板静止时，求它们的共同速度大小；
（2）某时刻木板速度是滑块的2倍，求此时滑块到木板最右端的距离；
（3）若滑块轻放在木板最右端的同时，给木板施加一水平向右的外力，使得木板保持匀速直线运动，直到滑块相对木板静止，求此过程中滑块的运动时间以及外力所做的功。
一列沿x轴正方向传播的简谐横波，其波源的平衡位置在坐标原点，波源在 内的振动图像如图（a）所示，已知波的传播速度为 。
（1）求这列横波的波长；
（2）求波源在4s内通过的路程；
（3）在图（b）中画出 时刻的波形图。
粤公网安备 44130202000953号