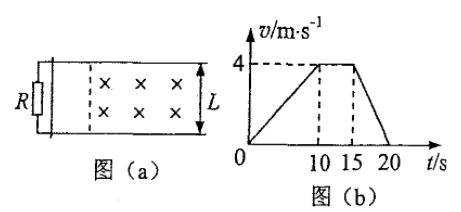
如图（a）两相距 的平行金属导轨固定于水平面上，导轨左端与阻值 的电阻连接，导轨间虚线右侧存在垂直导轨平面的匀强磁场，质量 的金属杆垂直于导轨上，与导轨接触良好，导轨与金属杆的电阻可忽略，杆在水平向右的恒定拉力作用下由静止开始运动，并始终与导轨垂直，其v-t图像如图（b）所示，在 时撤去拉力，同时使磁场随时间变化，从而保持杆中电流为0，求：
（1）金属杆所受拉力的大小为 ；
（2） 匀强磁场的磁感应强度大小为 ；
（3） 内磁感应强度随时间的变化规律。
在平面
直角坐标系xOy中，第Ⅰ象限存在沿y轴负方向的匀强电场，第Ⅳ象限存在垂直于坐标平面向外的匀强磁场，磁感应强度为B。一质量为m、电荷量为q的带正电的粒子从y轴正半轴上的M点以速度v0垂直于y轴射入电场，经x轴上的N点与x轴正方向成θ＝60°角射入磁场，最后从y轴负半轴上的P点垂直于y轴射出磁场，如图所示。不计粒子重力，求
（1）M、N两点间的电势差UMN ；
（2）粒子在磁场中运动的轨道半径r；
（3）粒子从M点运动到P点的总时间t。
如图，一直导体棒质量为m、长为l、电阻为r，其两端放在位于水平面内间距也为l的光滑平行导轨上，并与之密接；棒左侧两导轨之间连接一可控制的负载电阻（图中未画出）；导轨置于匀强磁场中，磁场的磁感应强度大小为B，方向垂直于导轨所在平面。开始时，给导体棒一个平行于导轨的初速度v0。在棒的运动速度由v0减小至v1的过程中，通过控制负载电阻的阻值使棒中的电流强度I保持恒定。导体棒一直在磁场中运动。若不计导轨电阻，求此过程中导体棒上感应电动势的平均值和负载电阻上消耗的平均功率。
如右图,一质量为M的物块静止在桌面边缘,桌面离水平地面的高度为h．一质量为m的子弹以水平速度v0射入物块后,以水平速度v0/2射出．重力加速度为g．求:
（1）此过程中系统损失的机械能；
（2）此后物块落地点离桌面边缘的水平距离．
如图所示,两个用轻线相连的位于光滑水平面上的物块,质量分别为m1和m2．拉力F1和F2方向相反,与轻线沿同一水平直线,且F1 > F2,试求在两个物块运动过程中轻线的拉力T．
板间电压及整个过程中粒子在磁场中运动的时间？
倍，并可以从Q点沿纸
面各个方向射入磁场，则粒子能打到CD边界的范围？
粤公网安备 44130202000953号