如图所示，两光滑金属导轨，间距d="0.2" m，在桌面上的部分是水平的，处在磁感应强度B="0.1" T、方向竖直向下的有界磁场中，电阻R="3" Ω，桌面高H="0.8" m，金属杆ab质量m="0.2" kg、电阻r="1" Ω，在导轨上距桌面h="0.2" m高处由静止释放，落地点距桌面左边缘的水平距离s="0.4" m，g="10" m/s2，求：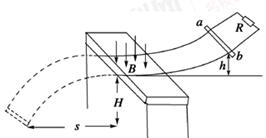
（1）金属杆刚进入磁场时，R上的电流大小；
（2）整个过程中R放出的热量．
相关试题
时间内的平均速度为
，紧接着
时间内的平均速度是
，则这段时间内的平均速度是多少？一列火车沿平直轨道运行，先以10米/秒的速度匀速行驶15分，随即改以15米/秒的速度匀速行驶10分，最后在5分钟又前进1000米而停止，则该火车在前25分钟及整个30分内的平均速度各为多大？
如图所示，光滑斜面倾角为
，一个重20N的物体在斜面上静止不动.轻质弹簧原长为10cm，现在的长度为6cm.
(1)求弹簧的劲度系数；
(2)若斜面粗糙，将这个物体沿斜面上移6cm，弹簧与物体相连，下端固定，物体仍静止于斜面上，求物体受到的摩擦力的大小和方向.
相关知识点
粤公网安备 44130202000953号