在平面直角坐标系中, 的区域存在着电场强度大小均为E的匀强电场,
的区域存在着电场强度大小均为E的匀强电场, 的部分电场沿x轴正向,
的部分电场沿x轴正向,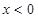 的区域电场沿x轴负向。
的区域电场沿x轴负向。 的区域存在一个矩形的垂直纸面向外的匀强磁场,磁感应强度大小为B。一个电荷量为q的正电荷从靠近y轴的第一象限内M点沿y轴负方向以初速度
的区域存在一个矩形的垂直纸面向外的匀强磁场,磁感应强度大小为B。一个电荷量为q的正电荷从靠近y轴的第一象限内M点沿y轴负方向以初速度 开始运动,恰好从N点进入磁场。已知电荷质量为m且不计重力,OM=2ON。
开始运动,恰好从N点进入磁场。已知电荷质量为m且不计重力,OM=2ON。
(1)N点坐标;
(2)若粒子经过磁场最后能无限靠近M点,则矩形区域的最小面积是多少;
(3)在(2)的前提下,该粒子由M点出发返回到无限靠近M点所需的时间。
在平面直角坐标系中, 的区域存在着电场强度大小均为E的匀强电场,
的区域存在着电场强度大小均为E的匀强电场, 的部分电场沿x轴正向,
的部分电场沿x轴正向,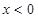 的区域电场沿x轴负向。
的区域电场沿x轴负向。 的区域存在一个矩形的垂直纸面向外的匀强磁场,磁感应强度大小为B。一个电荷量为q的正电荷从靠近y轴的第一象限内M点沿y轴负方向以初速度
的区域存在一个矩形的垂直纸面向外的匀强磁场,磁感应强度大小为B。一个电荷量为q的正电荷从靠近y轴的第一象限内M点沿y轴负方向以初速度 开始运动,恰好从N点进入磁场。已知电荷质量为m且不计重力,OM=2ON。
开始运动,恰好从N点进入磁场。已知电荷质量为m且不计重力,OM=2ON。
(1)N点坐标;
(2)若粒子经过磁场最后能无限靠近M点,则矩形区域的最小面积是多少;
(3)在(2)的前提下,该粒子由M点出发返回到无限靠近M点所需的时间。