如图所示,空间有一个范围足够大的匀强磁场,磁感应强度为B,一个质量为m、电荷量为+q的带电小圆环套在一根固定的绝缘竖直细杆上,杆足够长,环与杆的动摩擦因数为μ。现使圆环以初速度v0向上运动,经时间t圆环回到出发位置。不计空气阻力。已知重力加速度为g。求当圆环回到出发位置时速度v的大小。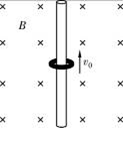
如图所示,空间有一个范围足够大的匀强磁场,磁感应强度为B,一个质量为m、电荷量为+q的带电小圆环套在一根固定的绝缘竖直细杆上,杆足够长,环与杆的动摩擦因数为μ。现使圆环以初速度v0向上运动,经时间t圆环回到出发位置。不计空气阻力。已知重力加速度为g。求当圆环回到出发位置时速度v的大小。