如图所示，在光滑水平地面上有一质量为2m的长木板，其左端放有一质量为m的重物（可视为质点），重物与长木板之间的动摩擦因数为。开始时，长木板和重物都静止，现在给重物一初速度v0，已知长木板撞到前方固定的障碍物时，长木板和重物的速度恰好相等，长木板与障碍物发生碰撞时不损失机械能，重物始终不从长木板上掉下来。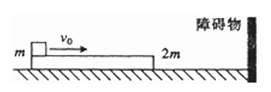
（1）求长木板与前方固定的障碍物相撞时的速度的大小；
（2）求长木板撞到前方固定的障碍物前运动的位移大小；
（3）求重物最终在长木板上相对滑动的距离大小。
如图所示，离子源A产生的初速度为零、带电量均为q，质量不同的正离子，被电压为U0的加速电场加速后匀速通过准直管，垂直射入平行板间的匀强偏转电场，偏转后通过极板HM上的小孔S离开电场，经过一段匀速直线运动，垂直于边界MN进入磁感应强度为B的匀强磁场，已知∠MNQ=90°，HO=d，HS=2d。（忽略粒子所受重力）
（1）求偏转电场场强E0的大小以及HM与MN的夹角
；
（2）求质量为m的正离子在磁场中做圆周运动的半径；
（3）若质量为9m的正离子恰好垂直打在NQ的中点S1处，试求能打在边界NQ上的正离子的质量范围。
某校物理兴趣小组决定举行遥控赛车比赛。比赛路径如图所示，赛车从起点A出发，沿水平直线轨道运动L后，由B点进入半径为R的光滑竖直圆轨道，离开竖直圆轨道后继续在光滑平直轨道上运动到C点，并能越过壕沟。已知赛车质量m=0.1kg，通电后以额定功率P=1.5W工作，进入竖直轨道前受到阻力恒为0.3N，随后在运动中受到的阻力均可不计。图中L=10.00m，R=0.32m，h=1.25m，s=1.50m。问：要使赛车完成比赛，电动机至少工作多长时间？（取g=10m/s2）
如图所示，绝缘轨道由弧形轨道和半径为R=0.16m的圆形轨道、水平轨道连接而成，处于竖直面内的匀强电场中，PQ左右两侧电场方向相反，其中左侧方向竖直向下，场强大小均为103V/m，不计一切摩擦。质量为m=0.1kg的带正电小球可看作质点。从弧形轨道某处由静止释放，恰好能通过圆形轨道最高点，小球带电荷量q="1." 0×10-3C，g取10m/s2。求：
（1）小球释放点的高度h；
（2）若PQ右侧某一区域存在垂直纸面向里的匀强磁场（图中未画出），磁感应强度B=4
×102T，小球通过圆形轨道后沿水平轨道运动到P点进入磁场，从竖直边界MN上的A点离开时速度方向与电场方向成30o，已知PQ、MN边界相距L=0.7m，求：
①小球从P到A经历的时间；
②若满足条件的磁场区域为一矩形，求最小的矩形面积。
如图所示，两足够长的平行光滑的金属导轨MN、PQ相距为L，导轨平面与水平面的夹角
，导轨电阻不计，整个装置处于垂直于导轨平面向上的匀强磁场中。长为L的金属棒垂直于MN、PQ放置在导轨上，且始终与导轨接触良好，金属棒的质量m、电阻为R。两金属导轨的上端连接一个电阻，其阻值也为R。现闭合开关K ，给金属棒施加一个方向垂直于杆且平行于导轨平面向上的、大小为F＝2mg的恒力，使金属棒由静止开始运动，若金属棒上滑距离为s时速度恰达到最大，最大速度vm。（重力加速度为g， sin37°=0.6,cos37°=0.8）求：
（1）求金属棒刚开始运动时加速度大小；
（2）求匀强磁场的磁感应强度的大小；
（3）求金属棒由静止开始上滑2s的过程中，金属棒上产生的电热Q1。
如甲图所示，水平光滑地面上用两颗钉子（质量忽略不计）固定停放着一辆质量为M=2kg的小车，小车的四分之一圆弧轨道是光滑的，半径为R=0.6m，在最低点B与水平轨道BC相切，视为质点的质量为m=1kg的物块从A点正上方距A点高为h=1.2m处无初速下落，恰好落入小车圆弧轨道滑动，然后沿水平轨道滑行恰好停在轨道末端C。现去掉钉子（水平面依然光滑未被破坏）不固定小车，而让其左侧靠在竖直墙壁上，该物块仍从原高度处无初速下落，如乙图所示。不考虑空气阻力和物块落入圆弧轨道时的能量损失，已知物块与水平轨道BC间的动摩擦因数为μ=0.1，重力加速度g取10 m/s2，求：
（1）水平轨道BC长度；
（2）小车不固定时物块再次与小车相对静止时距小车B点的距离；
（3）两种情况下由于摩擦系统产生的热量之比。
粤公网安备 44130202000953号