如图所示，某人用轻绳牵住一只质量
=0.6kg的氢气球，因受水平风力的作用，系氢气球的轻绳与水平方向成
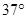角。已知空气对气球的浮力为15N，人的质量
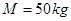，且人受的浮力忽略。（sin370=0.6，cos370=0.8，g＝10m/s2）求：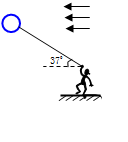
（1）在答卷上画出气球的受力分析图，并求出水平风力的大小
（2）通过计算说明，若水平风力增强，人对地面的压力如何变化？
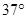如图所示，某人用轻绳牵住一只质量=0.6kg的氢气球，因受水平风力的作用，系氢气球的轻绳与水平方向成角。已知空气对气球的浮力为15N，人的质量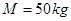，且人受的浮力忽略。（sin370=0.6，cos370=0.8，g＝10m/s2）求：
（1）在答卷上画出气球的受力分析图，并求出水平风力的大小
（2）通过计算说明，若水平风力增强，人对地面的压力如何变化？
粤公网安备 44130202000953号