在平面直角坐标系xOy中，第Ⅰ象限存在沿y轴负方向的匀强电场，第Ⅳ象限存在垂直于坐标平面向外的匀强磁场，磁感应强度为B.一质量为m、电荷量为q的带正
电的粒子从y轴正半轴上的M点以一定的初速度垂直于y轴射入电场，经x轴上的N点与x轴正方向成θ＝60°角射入磁场，最后从y轴负半轴上的P点垂直于y轴射出磁场，已知ON=d,如图所示.不计粒子重力，求：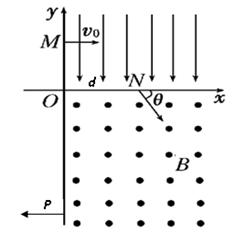
（1）粒子在磁场中运动的轨道半径R；
（2）粒子在M点的初速度v0的大小;
（3）粒子从M点运动到P点的总时间t.
(12分)如图所示，质量为m，电荷量为e的电子，从A点以速度v0垂直于电场方向射入一个电场强度为E的匀强电场中，从B点射出电场时的速度方向与电场线成120°角，电子重力不计。求：
(1)电子在电场中的加速度大小a及电子在B点的速度大小vB?
(2)A、B两点间的电势差UAB?
(3)电子从A运动到B的时间tAB?
如图所示，两条互相平行的光滑金属导轨位于水平面内，距离为L＝0.2米，在导轨的一端接有阻值为R＝0.5欧的电阻，在
0处有一与水平面垂直的均匀磁场，磁感强度B＝0.5T，一质量为m＝0.1千克的金属杆垂直放置在导轨上，并以v0＝2米／秒的初速度进入磁场，在安培力和一垂直于杆的水平外力F的共同作用下做匀变速直线运动，加速度大小为a＝2米／秒2、方向与初速度方向相反，设导轨和金属杆的电阻都可以忽略，且接触良好，求：
（1）电流为零时金属杆所处的位置；
（2）电流为最大值的一半时施加在金属杆上外力F的大小和方向；
（3）保持其它条件不变，而初速度v0取不同值，求开始时F的方向与初速度v0取值的关系。
一列正弦横波在
轴上传播，
、
是x轴上相距
m的两质点，
时，b点正好振动到最高点，而a点恰好经过平衡位置向上运动，已知这列波的频率为25Hz。
（1）设、在轴上的距离小于一个波长，试求出该波的波速。
（2）设、在轴上的距离大于一个波长，试求出该波的波速
如图所示为交流发电机示意图，匝数为
匝的矩形线圈，边长分别为l0cm和20cm，内阻为5
，在磁感强度B=0.5T的匀强磁场中绕
轴以
的角速度匀速转动，线圈和外部20电阻R相接，求：
（1）S断开时，电压表示数；
（2）S闭合时，电流表示数；
（3）发电机正常工作时，通过电阻R的电流最大值是多少？R上所消耗的电功率是多少？
（4）线圈从图示位置转过90°的过程中，通过电阻R的电量为多少？
。MN是一条通过球心的直线，单色细光束AB平行于MN射向球体，B为入射点，AB与MN间距为
cm，CD为出射光线。
。（需写出求解过程）
粤公网安备 44130202000953号