如图所示,质量为m的小球沿光滑的水平面冲上一光滑的半圆形轨道,轨道半径为R,小球在轨道最高点对轨道压力等于0.5mg,重力加速度为g,求: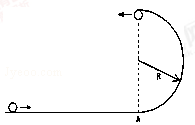
(1)小球在最高点的速度大小;
(2)小球落地时,距最高点的水平位移大小;
(3)小球经过半圆轨道最低点时,对轨道的压力.
相关知识点
如图所示,质量为m的小球沿光滑的水平面冲上一光滑的半圆形轨道,轨道半径为R,小球在轨道最高点对轨道压力等于0.5mg,重力加速度为g,求:
(1)小球在最高点的速度大小;
(2)小球落地时,距最高点的水平位移大小;
(3)小球经过半圆轨道最低点时,对轨道的压力.