如图所示,两个截面积均为S的圆柱形容器,左右两边容器高均为 ,右边容器上端封闭,左边容器上端是一个可以在容器内无摩擦滑动的轻活塞(重力不计),两容器由装有阀门的极细管道(体积忽略不计)相连通。开始时阀门关闭,左边容器中装有热力学温度为
,右边容器上端封闭,左边容器上端是一个可以在容器内无摩擦滑动的轻活塞(重力不计),两容器由装有阀门的极细管道(体积忽略不计)相连通。开始时阀门关闭,左边容器中装有热力学温度为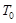 的理想气体,平衡时活塞到容器底的距离为
的理想气体,平衡时活塞到容器底的距离为 ,右边容器内为真空。现将阀门缓慢打开,活塞便缓慢下降,直至系统达到平衡,此时被封闭气体的热力学温度为T,且
,右边容器内为真空。现将阀门缓慢打开,活塞便缓慢下降,直至系统达到平衡,此时被封闭气体的热力学温度为T,且 >
> 。求此过程中外界对气体所做的功。(已知大气压强为P0)
。求此过程中外界对气体所做的功。(已知大气压强为P0)
如图所示,两个截面积均为S的圆柱形容器,左右两边容器高均为 ,右边容器上端封闭,左边容器上端是一个可以在容器内无摩擦滑动的轻活塞(重力不计),两容器由装有阀门的极细管道(体积忽略不计)相连通。开始时阀门关闭,左边容器中装有热力学温度为
,右边容器上端封闭,左边容器上端是一个可以在容器内无摩擦滑动的轻活塞(重力不计),两容器由装有阀门的极细管道(体积忽略不计)相连通。开始时阀门关闭,左边容器中装有热力学温度为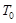 的理想气体,平衡时活塞到容器底的距离为
的理想气体,平衡时活塞到容器底的距离为 ,右边容器内为真空。现将阀门缓慢打开,活塞便缓慢下降,直至系统达到平衡,此时被封闭气体的热力学温度为T,且
,右边容器内为真空。现将阀门缓慢打开,活塞便缓慢下降,直至系统达到平衡,此时被封闭气体的热力学温度为T,且 >
> 。求此过程中外界对气体所做的功。(已知大气压强为P0)
。求此过程中外界对气体所做的功。(已知大气压强为P0)