如图所示，一物体M从A点以某一初速度沿倾角α=37°的粗糙固定斜面向上运动，自顶端B点飞出后，垂直撞到高H=2.25m的竖直墙面上C点，又沿原轨迹返回．已知B、C两点的高度差h＝0.45m，物体M与斜面间的动摩擦因数μ=0.25，取sin37°=0.6，cos37°=0.8，重力加速度g="10" m/s2．试求：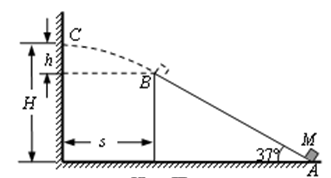
（1）物体M沿斜面向上运动时的加速度大小；
（2）物体返回后B点时的速度；
（3）物体被墙面弹回后，从B点回到A点所需时间。
如图所示，一质量为m、带电量为q的小球，用绝缘细线悬挂在水平向右的匀强电场中，静止时悬线向左与竖直方向成θ角，重力加速度为g。
（1）判断小球带何种电荷。
（2）求电场强度E。
如图所示，可视为质点的滑块B放在水平面上，在其正上方离水平面高h=0.8m处有一可视为质点的小球A，某时刻A以v1=5m/s开始向右做平抛运动，同时B以v2=3m/s的初速度开始向右做匀加速直线运动，A恰好能击中B，求B运动的加速度的大小a。（g=10m/s2）
(12分)如图所示，物体A放在某一水平面上，已知物体A重60N，A与水平面之间的动摩擦因数为μ=0.3，A、B均处于静止状态，绳AC水平，绳CD与水平方向成37°角，CD绳上的拉力为15N. sin37°=0.6，cos37°=0.8．求：
（1）物体A受到的摩擦力为多大？
（2）物体B重力为多大？
汽车先以a1=0.5m/s2的加速度由静止开始做匀加速直线运动，在20s末改做匀速直线运动，当匀速运动持续10s后，因遇到障碍汽车便紧急刹车，已知刹车的加速度为a2=－2m/s2,求：
（1）汽车匀速运动时的速度大小；
（2）汽车刹车后6s内所通过的位移大小；
（3）在坐标图上画出该汽车运动全过程的速度-时间图象。
粤公网安备 44130202000953号