如图所示，质量为m的小物块放在长直水平面上，用水平细线紧绕在半径为R、质量为2m的薄壁圆筒上．t=0时刻，圆筒在电动机带动下由静止开始绕竖直中心轴转动，转动中角速度满足ω=βt（β为已知常数），物块和地面之间动摩擦因数为μ．求：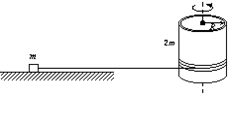
（1）物块运动中受到的拉力．（2）从开始运动至t=t1时刻，电动机对物块做了多少功？
如图所示，两平行金属板A、B长度l=0.8m，间距d=0.6m．直流电源E能提供的最大电压为9×105V，位于极板左侧中央的粒子源可以沿水平方向向右连续发射比荷为=
l×107C/kg、重力不计的带电粒子，射人板间的粒子速度均为v0=4×106
m/s．在极板右侧有一个垂直纸面向里的匀强磁场，磁感应强度B=lT，分布在环带区域中，该环带的内外圆的圆心与两板间的中心重合于O点，环带的内圆半径Rl=
m．将变阻器滑动头由a向b慢慢滑动，改变两板间的电压时，带电粒子均能从不同位置穿出极板射向右侧磁场，且两板间电压最大时，对应的粒子恰能从极板右侧边缘穿出．
(1)问从板间右侧射出的粒子速度的最大值vm是多少?
(2)若粒子射出电场时，速度的反向延长线与v0所在直线交于O/点，试用偏转运动相关量证明O/点与极板右端边缘的水平距离x=
，即O/与0重合，所有粒子都好像从两板的中心射 出一样．
(3)为使粒子不从磁场右侧穿出，求环带磁场的最
小宽度d.
一辆汽车质量为3×103kg ，额定功率为8×104W，发动机的最大牵引力为8×103N ．该汽车在水平路面由静止开始做直线运动,运动中所受阻力恒定．汽车匀加速直线运动所能达到的速度为v1,之后做变加速运动，达到的最大速度为v2．其行驶过程中牵引力F与车速的倒数
的关系如图所示．求:
（1）运动过程中汽车所受阻力和最大速度v2的大小；
（2）汽车匀加速直线运动中的加速度的大小；
（3）该汽车由静止开始运动，经过85s达到最大速度，求汽车在BC段所对应的位移的大小。
如图所示，一轻质弹簧竖直固定在水平地面上，将一个质量为m的物块P轻轻地放在弹簧上，当弹簧被压缩l时物块速度刚好为零，若换一个质量为3m的
物块Q轻轻地放在弹簧上，当弹簧也被压缩l时，物块Q的加速度和速度的大小分别是多少？
如图甲所示，带正电的粒子以水平速度v0从平行金属板MN间中线
连续射入电场中，MN板间接有如图乙所示的随时间t变化的电压
，电压变化周期T=0.1s，两板间电场可看做均匀的，且两板外无电场. 紧邻金属板右侧有垂直纸面向里的匀强磁场B，分界线为CD，AB为荧光屏. 金属板间距为d，长度为l，磁场B的宽度为d. 已知：
，带正电的粒子的比荷为q/m=108C/kg，重力忽略不计. 试求：
（1）带电粒子进入磁场做圆周运动的最小半径；
（2）带电粒子射出电场时的最大速度；
（3）带电粒子打在荧光屏AB上的范围.
，某时刻，对B施加一个向右的水平恒力F=
，使系统由静止开始运动，当A盒右边缘与墙相撞时，撤去力F，此时B恰好与A右壁相碰。已知A和墙碰撞后速度变为零但不粘连，A和B碰撞过程无机械能损失，假设碰撞时间均极短，求整个过程中：
粤公网安备 44130202000953号