如图所示，一质量M=3kg的足够长木板B静止于光滑水平面上，B的右边放有竖直挡板，B的右端距挡板S=4m。现有一小物体A（可视为质点）质量m=1kg，以速度v0=8m/s从B的左端水平滑上B，已知A和B 间的动摩擦因数μ=0.2，B与竖直挡板的碰撞时间极短，且碰撞时无机械能损失。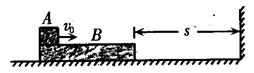
求：（1）B与竖直挡板碰撞前的速度是多少？
（2）若题干中的S可以任意改变（S不能为零）大小，要使B第一次碰墙后，AB系统动量为零，S的大小是多少？
（3）若要求B与墙碰撞两次，B的右端距挡板S应该满足什么条件？
相关试题
如图所示，质量M =10kg，倾角θ =37°的斜面体静止在粗糙的水平地面上，斜面体和水平面间的动摩擦因数µ =0.04。一质量m =2kg的物体由静止开始沿斜面下滑，沿斜面下滑2m时物体的速度为v =2m/s，此过程中，斜面体一直处于静止状态。求：
（1）地面对斜面体的摩擦力大小；
（2）地面对斜面体的支持力大小。
如图所示，光滑水平面上A、B两小球沿同一方向运动，A球的动量为4kgm/s，B球的质量为1kg，速度为6m/s，已知两球相碰后，A球的动量减为原来的一半，方向与原方向一致。求：
（1）碰撞后B球的速度变为多大?
（2）A球的质量范围。
粤公网安备 44130202000953号