同学们学习了《伽利略对自由落体运动的研究》后,老师给大家出了这样一道题:假设有人把一个物体从比萨斜塔塔顶无初速落下(不考虑空气阻力),物体到达地面前最后一秒内通过的位移为整个位移的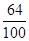 ,求塔高H(取g=10 m/s2)。有同学给出的解法:根据h=
,求塔高H(取g=10 m/s2)。有同学给出的解法:根据h=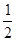 gt2得物体在最后1 s内的位移h1=
gt2得物体在最后1 s内的位移h1=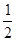 gt2=5 m,再根据
gt2=5 m,再根据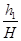 =
= ;得H=7.81m,这位同学的解法是否正确?如果正确说明理由,如果不正确请给出正确解析过程和答案。
;得H=7.81m,这位同学的解法是否正确?如果正确说明理由,如果不正确请给出正确解析过程和答案。
同学们学习了《伽利略对自由落体运动的研究》后,老师给大家出了这样一道题:假设有人把一个物体从比萨斜塔塔顶无初速落下(不考虑空气阻力),物体到达地面前最后一秒内通过的位移为整个位移的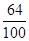 ,求塔高H(取g=10 m/s2)。有同学给出的解法:根据h=
,求塔高H(取g=10 m/s2)。有同学给出的解法:根据h=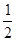 gt2得物体在最后1 s内的位移h1=
gt2得物体在最后1 s内的位移h1=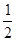 gt2=5 m,再根据
gt2=5 m,再根据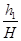 =
= ;得H=7.81m,这位同学的解法是否正确?如果正确说明理由,如果不正确请给出正确解析过程和答案。
;得H=7.81m,这位同学的解法是否正确?如果正确说明理由,如果不正确请给出正确解析过程和答案。