如图所示，半径R=1m的光滑绝缘的1/4圆弧与水平绝缘的传送带相切且相接与B点，传送带的顺时针运行，速度恒为v0=1m/s，长L=2.875m。在整个空间中加上水平向左的匀强电强E= 2×104V/m，现将质量m=1kg，电量q=+1.0×10-4C的滑块从A点（A点与圆心O点等高）无初速度释放。已知滑块与传送带间的动摩擦因数为μ=0.1，g=10m/s2，试求：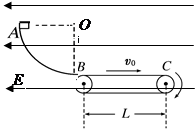
（1）滑块滑到B点时的速度大小？
（2）滑块在传送带上运动时间？
（3）滑块在传送带上运动摩擦生的热Q？
如图所示，半径R=0.9m的光滑的半圆轨道固定在竖直平面内，直径AC竖直，下端A与光滑的水平轨道相切。一小球沿水平轨道进入竖直圆轨道，通过最高点C时对轨道的压力为其重力的3倍。不计空气阻力，g取10m/s2。求：
（1）小球在A点的速度大小；
（2）小球的落地点到A点的距离。
如图所示，质量为1kg的小物块以5m/s的初速度滑上一块原来静止在水平面上的木板，木板质量为4kg，木板与水平面间的动摩擦因数为0.02，经时间2s后，小物块从木板另一端以1m/s相对于地的速度滑出，g=10m/s2，求这一过程中木板的位移和系统在此过程中因摩擦增加的内能.
两个氘核发生了如下核反应：
，其中氘核质量为2.1036u，氢核质量为3.1050u，中子质量为1.0087u。求：
①核反应中释放的核能。
②在两个氘核以相等的动能0.35MeV进行对心碰撞，并且核能全部转化为机械能的情况下，求反应中产生的中子和氦核的动能。
③假设反应中产生的氦核沿直线向原来静止的碳核(
C)接近，受库仑力的影响，当它
们的距离最近时，两个原子核的
动能各是多少?
和
，且某物理兴趣小组想测量太阳辐射的功率，其做法是取一个横截面积是3×10—2m2的不高的圆筒，筒内装满0.6kg的水。某天中午在太阳光的照射下，测得2分钟后水温升高了1℃ 。该小组同学已经查的资料有下列一些：
| R地=6400km |
M地=5.97×1024kg |
Q=CmΔt |
射到地球大气层顶层的太阳能只有43℅达到地面，另外57℅被大气吸收或反射而未到达地面 |
| R日地=1.5×108km |
太阳质量：1.9891 × 1030 kg |
ΔU=W+Q |
|
| 水的密度: 1.0×103kg/m3 |
水的比热： 4.2×103J/(kg.℃) |
球的表面积： S=4πr2 |
根据上述资料和实验数据计算：
（1）在阳光直射下，地球
表面每平方厘米的面积上每分钟获得的能量
（2）估算太阳辐射的功率（保留两位有效数字）
粤公网安备 44130202000953号